Test: Regular Expressions & Finite Automata- 3 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Regular Expressions & Finite Automata- 3
Consider the following languages
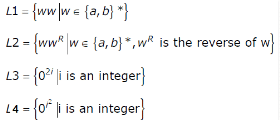
Q. Which of the languages are regular?
Let S and T be language over Σ = {a,b} represented by the regular expressions (a+b*)* and (a+b)*, respectively. Which of the following is true?
Let L denotes the language generated by the grammar S -> 0S0/00. Which of the following is true?
What can be said about a regular language L over {a} whose minimal finite state automaton has two states?
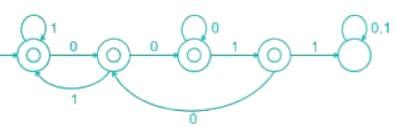
Consider the following Deterministic Finite Automata
Q. Which of the following is true?
How many minimum states are required in a DFA to find whether a given binary string has odd number of 0's or not, there can be any number of 1's.
Consider the DFAs M and N given above. The number of states in a minimal DFA that accepts the language L(M) ∩ L(N) is __________.
Consider alphabet ∑ = {0, 1}, the null/empty string λ and the sets of strings X0, X1 and X2 generated by the corresponding non-terminals of a regular grammar. X0, X1 and X2 are related as follows:
X0 = 1 X1
X1 = 0 X1 + 1 X2
X2 = 0 X1 + {λ}
Q. Which one of the following choices precisely represents the strings in X0?
Which of the following languages is/are regular?
L1: {wxwR ⎪ w, x ∈ {a, b}* and ⎪w⎪, ⎪x⎪ >0} wR is the reverse of string w
L2: {anbm ⎪m ≠ n and m, n≥0
L3: {apbqcr ⎪ p, q, r ≥ 0}
The number of states in the minimal deterministic finite automaton corresponding to the regular expression (0 + 1)*(10) is ____________
Let T be the language represented by the regular expression Σ∗0011Σ∗ where Σ = {0, 1}. What is the minimum number of states in a DFA that recognizes L' (complement of L)?
Which one of the following regular expressions is NOT equivalent to the regular expression (a + b + c) *?
Which one of the following strings is not a member of L (M)?
Let L be a regular language and M be a context-free language, both over the alphabet Σ. Let Lc and Mc denote the complements of L and M respectively. Which of the following statements about the language Lc∪ Mc is TRUE
Which of the following statements is TRUE about the regular expression 01*0?
The language {0n 1n 2n | 1 ≤ n ≤ 106} is
Consider the non-deterministic finite automaton (NFA) shown in the figure.
State X is the starting state of the automaton. Let the language accepted by the NFA with Y as the only accepting state be L1. Similarly, let the language accepted by the NFA with Z as the only accepting state be L2. Which of the following statements about L1 and L2 is TRUE? Correction in Question: There is an edge from Z->Y labeled 0 and another edge from Y->Z labeled 1 - in place of double arrowed and no arrowed edges.
A language L satisfies the Pumping Lemma for regular languages, and also the Pumping Lemma for context-free languages. Which of the following statements about L is TRUE?
Consider the context-free grammar E → E + E E → (E * E) E → id
where E is the starting symbol, the set of terminals is {id, (,+,),*}, and the set of nonterminals is {E}.
Q. Which of the following terminal strings has more than one parse tree when parsed according to the above grammar?
Consider the context-free grammar E → E + E E → (E * E) E → id
where E is the starting symbol, the set of terminals is {id, (,+,),*}, and the set of non-terminals is {E}. For the terminal string id + id + id + id, how many parse trees are possible?
|
55 docs|215 tests
|
|
55 docs|215 tests
|