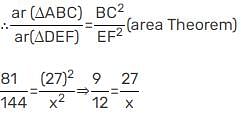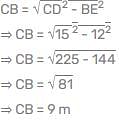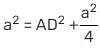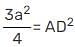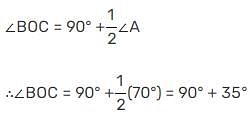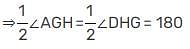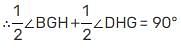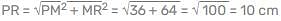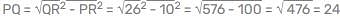MCQ: Geometry - 2 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Geometry - 2
In the given figure ∠BAD = ∠CAD. AB = 4 cm, AC = 5.2 cm, BD = 3 cm. Find BC.
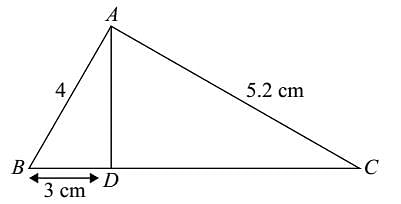

In the given figure, DE || BC if AD = 1.7 cm, AB = 6.8 cm and AC = 9 cm, find AE.
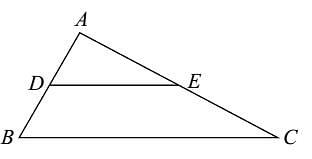

The areas of two similar Δs are 81 cm2 and 144 cm2. If the largest side of the smaller Δ is 27 cm, then the largest side of the larger Δ is :
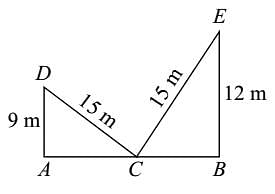
A ladder 15 m long reaches a window which is 9 m above the ground on one side of street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 12 m high. What is the width of the street:
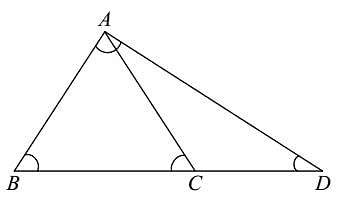
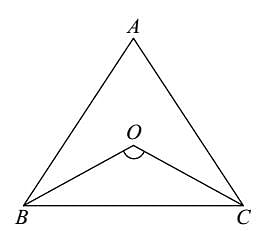
In ΔABC, the angle bisectors of ∠B and ∠C meet at O. If ∠A = 70°, then ∠BOC is equal to:
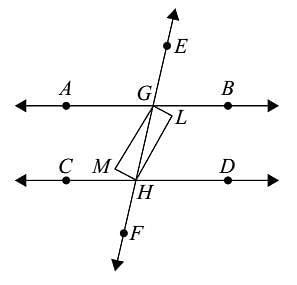
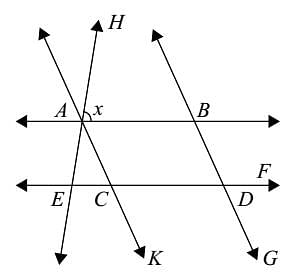
In the given figure, AB || CD and AC || BD. If ∠EAC = 40°, ∠FDG = 55°, ∠HAB = x; then the value of x is:
If two parallel lines are intersected by a transversal, then the bisectors of the two pairs of interior angles enclose a:
The complement of an angle exceeds the angle by 60°. Then the angle is equal to:
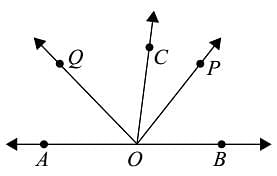
In the given figure, OP bisect ∠BOC and OQ bisects ∠AOC. Then ∠POQ is equal to :
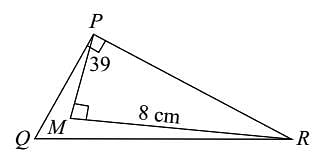
In the given figure ∠QPR = 90°, QR = 26 cm, PM = 6 cm, MR = 8 cm and ∠PMR = 90°, find the area of ΔPQR.
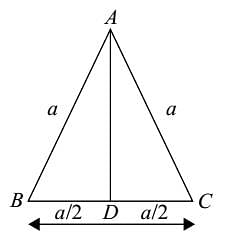
In, ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
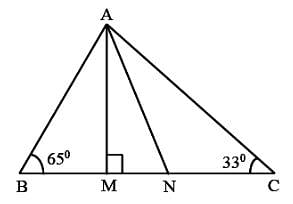
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. What is the measure of ∠MAN.
|
314 videos|170 docs|185 tests
|