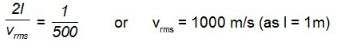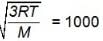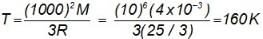IIT JAM Physics MCQ Test 6 - Physics MCQ
30 Questions MCQ Test IIT JAM Physics Mock Test Series 2026 - IIT JAM Physics MCQ Test 6
For an LCR circuit having resonant frequency f0 and bandwidths B1 match List I with List II and select the correct answer using the codes given below the Lists:


An oscillating voltage V(t) = V0 sin ωt is applied across a parallel plate capacitor having a plate separation d. The displacement current density through the capacitor is


A power (step-up) transformer with 1:8 turn ratio has 60 Hz, 120V across the primary, the load in the secondary is 104Ω. The current in the secondary is:-
An alternating potential (V) = V sin cot is applied across a circuit. As a result the current 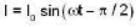 flows in it. The power consumed in the circuit per cycle is:-
flows in it. The power consumed in the circuit per cycle is:-
An ideal inductor takes current of 10 A when connected to a 125 V. 50 Hz ac supply. A pure resistor across the same source takes 12.5 A. If the two are connected in series across a 100 √2 v, 40 Hz supply, the current through the circuit will be
For a varying current 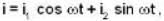 the R.M.S. value of current will be:
the R.M.S. value of current will be:
A circular loop of radius a' is made of single form of thin conducting wire. The self inductance of this loop is L'. If the no. of turns in the loop is increased from 1 to 8. the self inductance would be:-
An LR circuit with a battery is connected at t = 0, which of the following quantities is/are not zero just after the connection?
Which one of the following Maxwell's equations implies the absence of magnetic monopoles?
In a homogeneous non conducting region where  the value of ε1
the value of ε1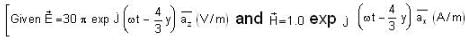 will be
will be
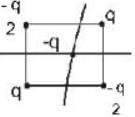
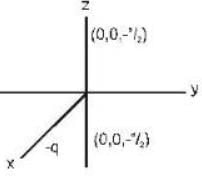
Positive and negative point charges of equal magnitude are kept at 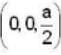 and
and  respectively.
respectively.
The work done by the electric field when another positive point charge in moved from (-a. 0. 0) to (0. a. 0) is
A certain charge Q is divided into two parts q and (Q - q). For the maximum coulomb force between them, the ratio (q/Q) is:
A charge situated at a certain distance from an electric dipole in the end on position experiences a force F. If the distance of the charge is doubled, the force acting on the charge will be:
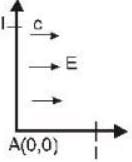
A uniform electric field pointing in positive x-direction exists in a region. Let A be the origin. B be the point on the x-axis at = +1 cm and c be point on the y - axis at y = +1 cm. Then the potentials at the points A. B and C satisfy:
A disk of radius a/4 having a uniformly distributed charge 6C is placed 8c is placed on the x- axis from x =a/4 to x = 5a/4. Two point charge - 7 c and 3c are placed at (a/4. 0) and (-3a/4,3a/4.0), respectively, consider a cubical surface formed by six surfaces x = x = ±a/2.y = ±a/2.z = ±a/2. The electric flux through this cubical surface is
An electromagnetic wave whose electric field is given below

Ez= 0
Two long parallel wires of zero resistance are connected to each other by a battery of 1.0 V. The separation between the wires is 0.5 m. A metal bar, which is perpendicular to the wire and of resistance 10 Ω moves on these wires when a magnetic field of 0.02 tesla is acting perpendicular to the plane containing the bar and the wires. If the mass of the bar is 0.002 kg.
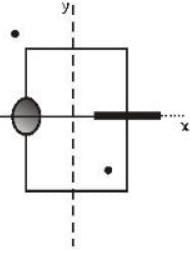
A conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field in a direction perpendicular to that of fixed diameter
Which of the following are correct if electrostatic potential field is given by 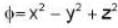
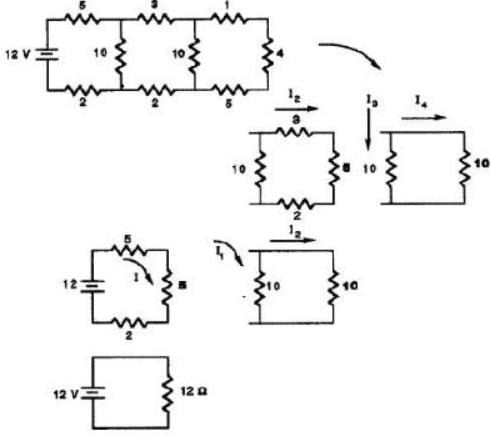
Consider the circuit shown below. Calculate the effective resistance of the circuit and use this knowledge to find the current (in Ampere) in the 4Ω resistor.
A potential difference of V is applied at the ends of a copper wire of length l and diameter d. On doubling only d, drift velocity
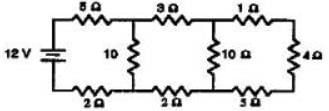
Calculate the equivalent resistance between points C & D in the combination of resistance shown in figure.
Assuming that all the energy from a 2000 watt lamp is radiated uniformly, calculate the average values of the intensities of electric fields (in v/m) of radiation at a distance of 2 m from the lamp.
Calculate the magnitude of poynting vector (in mega watt/m2) at the surface of the sun. Given that power radiated by sun is 4 * 1026 watts and radius of sun is 7 x 108m ).
A container of volume 1 m3 is divided into two equal parts by a partition. One part has an ideal gas at 300 K and the other part is vacuum. The whole system is thermally isolated from the surroundings. When the partition is removed, the gas expands to occupy the whole volume. Its temperature will now be ____ .
During an experiment, an ideal gas is found to obey an additional law p2V = constant. The gas is initially at a temperature T and volume V. When it expands to a volume 2V. the temperature becomes ____ .
One mole of a monoatomic ideal gas is mixed with one mole of a diatomic ideal gas. The molar specific heat of the mixture at constant volume is ____ .
Let four point charges  and -q/2 be placed at the verticies of a square of side a. Let another point charge -q be placed at the centre of the square Let v(r) be the electrostatic potential at a point P at a distance r » a from the centre of the square. Then
and -q/2 be placed at the verticies of a square of side a. Let another point charge -q be placed at the centre of the square Let v(r) be the electrostatic potential at a point P at a distance r » a from the centre of the square. Then  is_____.
is_____.
A cubical box of side 1 m contains helium gas (atomic weight 4) at a pressure of 100 N/m2. During an abservation time of 1 s, an atom travelling with the root mean square speed parallel to one of the edges of the cube, was found to make 500 his with a particular wall, without any collision other atoms. Take,  Evaluate the temperature of the gas.
Evaluate the temperature of the gas.
|
4 docs|21 tests
|



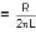
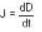

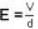
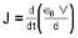


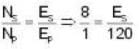
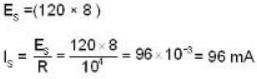



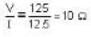

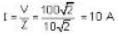
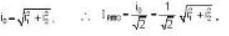
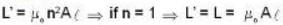
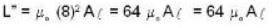
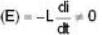
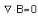 i.e. total flux through a surface is zero which provide the absence of magnetic monopoles.
i.e. total flux through a surface is zero which provide the absence of magnetic monopoles.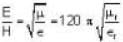 ...(i)
...(i)
 ...(ii)
...(ii)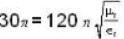
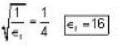
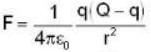
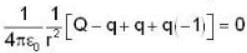
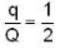
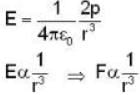
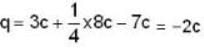
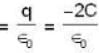
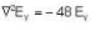
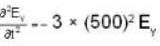
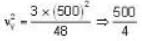
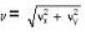

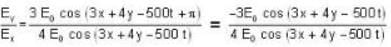

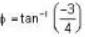
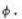
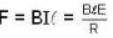 ...(i)
...(i) will be induced in it. Due to this induced emf, the induced current
will be induced in it. Due to this induced emf, the induced current  will result in a force
will result in a force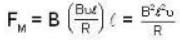 ...(ii)
...(ii)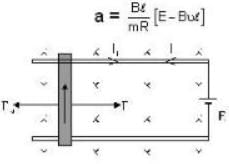

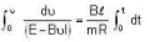
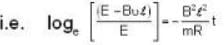
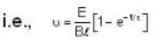 with
with 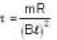 ..(iv)
..(iv)
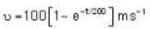 Ans.
Ans.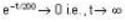
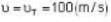
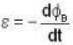 i.e the emf induced is equal to change in magnetic flux per unit time.
i.e the emf induced is equal to change in magnetic flux per unit time. If potential does not satisfies laplace equation then it satisfies Poisson equation.
If potential does not satisfies laplace equation then it satisfies Poisson equation.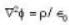



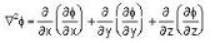
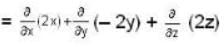
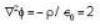
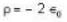 Ans.
Ans.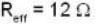
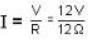
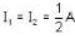
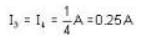
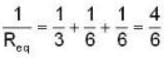
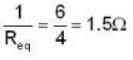

 EH (from poynting theorem)
EH (from poynting theorem)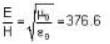
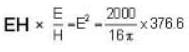

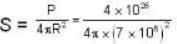
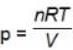 we have T2/V = constant
we have T2/V = constant 2R
2R

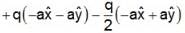
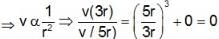
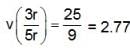

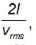 where l is the side of cube.
where l is the side of cube.