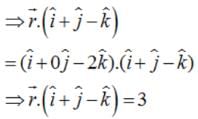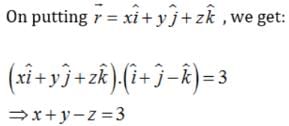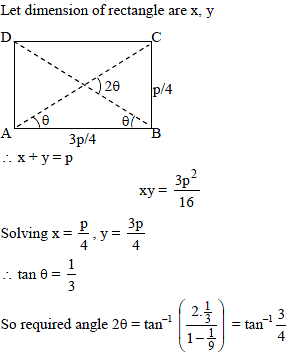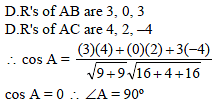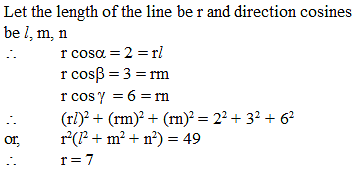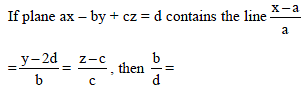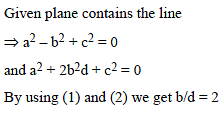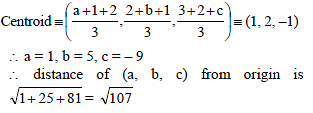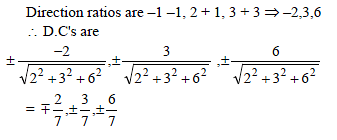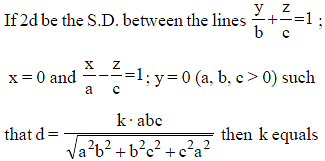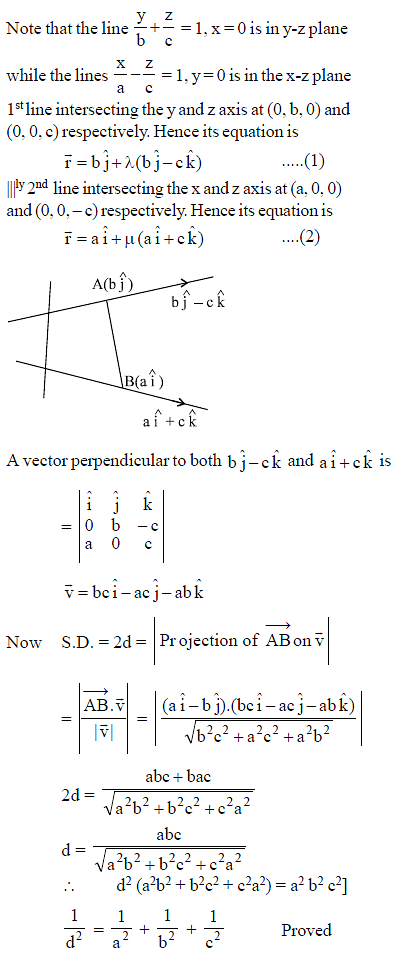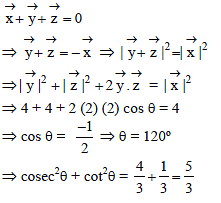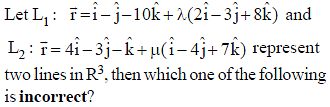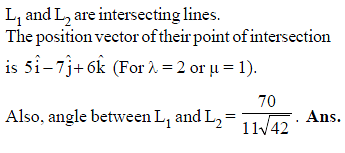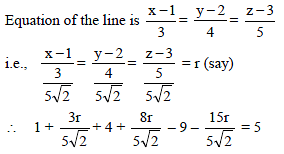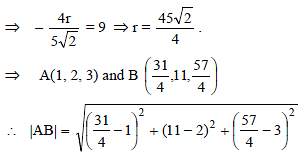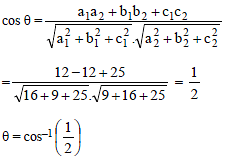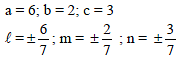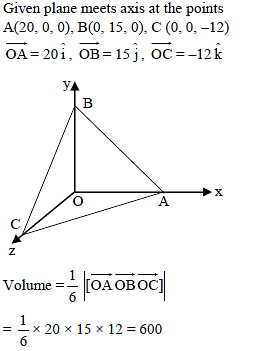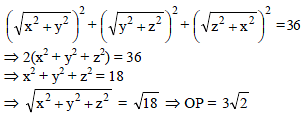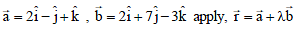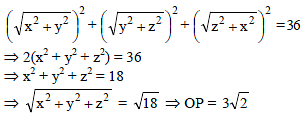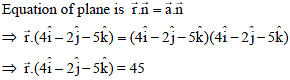Three Dimensional Geometry - 1 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Three Dimensional Geometry - 1
In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0
The equation of a plane through a point whose position vector is 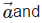 perpendicular to the vector
perpendicular to the vector 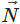 . is
. is
If l1, m1, n1 and l2, m2, n2 are the direction cosines of two lines; and θ is the acute angle between the two lines; then
Find the distance of the point (0, 0, 0) from the plane 3x – 4y + 12 z = 3
If a1, b1, c1 and a2, b2, c2 are the direction ratios of two lines and θ is the acute angle between the two lines; then
The vector and cartesian equations of the planes that passes through the point (1, 0, – 2) and the normal to the plane is
If the coordinates of point A, B, C are (–1, 3, 2), (2, 3, 5) and (3, 5, –2) respectively then angle A is
The projection of a line on the axes are 2, 3, 6 then the length of line is
OABC is a tetrahedron whose vertices are O(0, 0, 0) ; A(a, 2, 3) ; B(1, b, 2) and C(2, 1, c). If its centroid be (1, 2, –1) then distance of the point (a, b, c) from the origin is
Find the direction cosines of line joining points (1, –1, –3) and (–1, 2, 3)
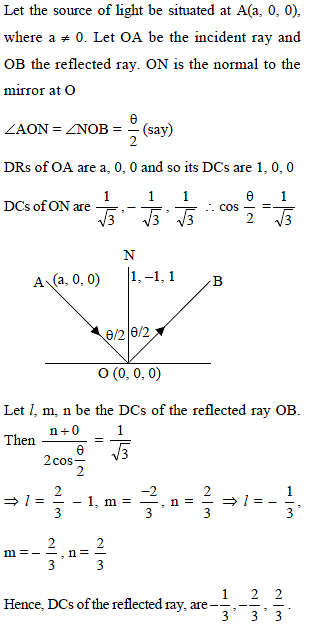
A mirror and a source of light are situated at the origin O and at a point on OX respectively. A ray of light from the source strikes the mirror and is reflected. If the DRs of the normal to the plane of mirror are 1, –1, 1, then DCs for the reflected ray are -
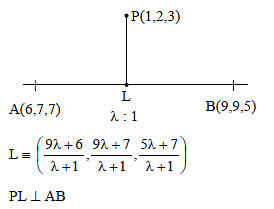
Foot of perpendicular from (1, 2, 3) to the line joining points (6, 7, 7) and (9, 9, 5) is-
If x + y + z = 0, | x | = | y | = | z | = 2 and θ is angle between y and z. then the value of cosec2θ + cot2θ is equal to
A line passing through A(1, 2, 3) and having direction ratios (3, 4, 5) meets a plane x + 2y – 3z = 5 at B, then distance AB is equal to-
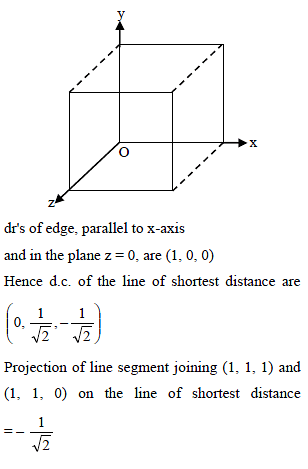
The shortest distance between a diagonal of a cube of edge-length one unit and the edge not meeting it, is -
Angle between the rays with d.r.'s 4, – 3, 5 & 3, 4, 5 is-
The direction cosines of the line joining the points (4, 3, –5) and (–2, 1, –8) are
The equation xy = 0 in three dimensional space represents -
The volume of the tetrahedron included between the plane 3x + 4y –5z – 60 = 0 and the coordinate planes in cubic units is
If the sum of the squares of the distance of a point from the three co-ordinate axes be 36, then its distance from the origin is
If the sum of the squares of the distance of a point from the three co-ordinate axes be 36, then its distance from the origin is
If the foot of perpendicular drawn from the origin to the plane is (4, – 2, – 5). Then equation of plane is
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|