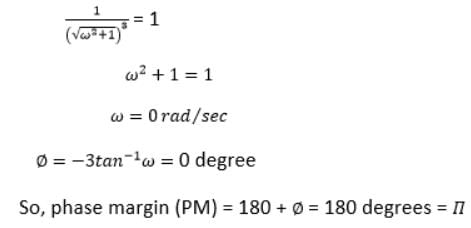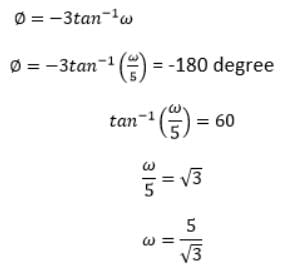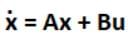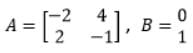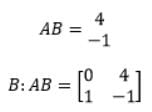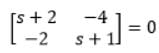Test: Control Systems - 3 - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: Control Systems - 3
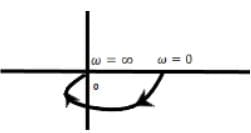
The phase margin of the given system G(s) = 1 / [(s + 1) 3] is:
The GM of a unity feedback system with the transfer function 1/ (s + 5)3 is:
What will be the controller output for PD controller at t = 2s, if the error begins to change from 0 at the rate of 1.2% /s? The given parameters are Po = 50%, Kp = 4, and KD = 0.4.
Consider the following statements:
1. Lead compensator increases the bandwidth of the system.
2. Lag compensator suppresses steady-state performance.
3. Lead compensator improves the dynamic response and provides faster response.
4. Lag compensator acts as a low-pass filter.
Of these above statements, which of the following are true?
Consider the following statements:
Phase lead:
(1) Increases the bandwidth of the system
(2) Improves the damping
(3) Reduces steady-state error
(4) Increases gain at high frequency
Which of the following statements are true?
The following set of differential equations describes a linear second-order single input continuous-time system.
X1'(t) = -2X1(t) + 4X2(t)
X2'(t) = 2X1(t) - X2(t) + u(t)
Here, X1(t) and X2(t) are the state variables, and u(t) is the control variable. Check for the system, if it is:
The transfer function of a compensating network is in the form of (1 +aTs) / (1 + Ts). Find the value of 'a' if the given network is the phase-lag network.
The controller required to handle fast process load changes is:
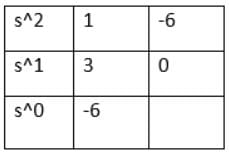
The characteristic equation of the feedback control system is given as: s3 + 4s2 + (K + 5)s + K = 0
Here, K is a scalable variable parameter. In the root loci diagram of the system, the asymptotes of the root locus for large values of K meet at a point in the s-plane whose coordinate is:
An open loop transfer function is given by G(s) = K (s + 1) / (s + 4)(s2 + 3s + 2). It has:
For the given closed-loop system, the ranges of the values of K for stability is:
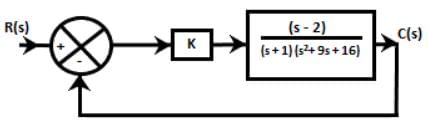
If s3 + Ks2 + 5s + 10 = 0, the root of the feedback system's characteristic equation is said to be critically stable. Then, the value of K will be: