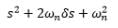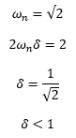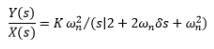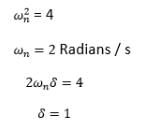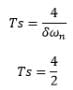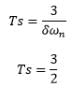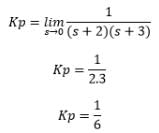Test: Control Systems - 2 - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: Control Systems - 2
A major part of the automatic control theory applies to the:
If the characteristic equation of the closed loop system is s2 + 2s + 2 = 0, then the system is:
The closed loop transfer function for a second order system is: T(s) = 4/ (s2 + 4s + 4). Calculate the settling time for a 2 percent and 5 percent band.
The step error coefficient of a system G(s) = 1/ (s+2)(s+3) with unity feedback is:
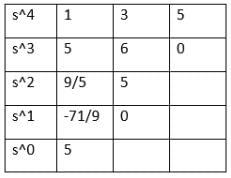
The number of roots in the left half of the s-plane of the given equation s3 + 3s2 + 4s + 1 = 0 is:
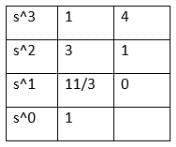
A system with the polynomial s4 + 5s3 + 3s2 + 6s + 5 = 0 is:
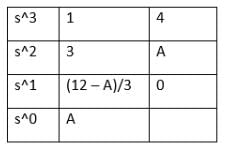
If s3 + 3s2 + 4s + A = 0, the roots of the characteristic equation lie in the left half of the s-plane. The value of the A is said to be:
Find the number of asymptotes for the given open-loop transfer function of a unity feedback system:
G(s) = ((s + 2) (s+3) (s + 4)) / ((s + 5) (s+6) (s + 1))
Calculate the centroid for the given system:
G(s) = K / [(s + 1) (s + 4 + 4j) (s + 4 - 4j)]
Determine the gain margin of the given open-loop feedback control system: G(s)H(s) = 1 / [(s + 1) 3]


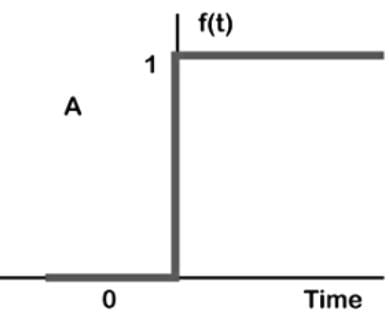

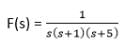
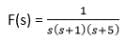 = A/s + B/ (s+1) + C/(s+5)
= A/s + B/ (s+1) + C/(s+5)