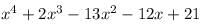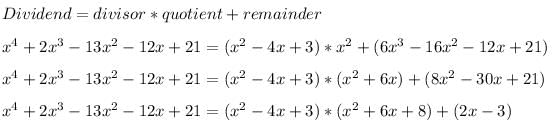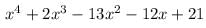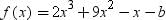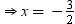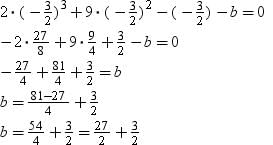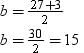Test: Division Algorithm for Polynomials - Class 10 MCQ
20 Questions MCQ Test Online MCQ Tests for Class 10 - Test: Division Algorithm for Polynomials
The expression that should be subtracted from the polynomial f(x) = x4 + 2x3-13x2 – 12x + 21 so that the resulting polynomial is exactly divisible by g(x) = x2 – 4x + 3 is
If (x + 1) is a factor of x2 – 3ax + 3a – 7, then the value of a is
The value of quadratic polynomial f (x) = 2x2– 3x- 2 at x = -2 is ……
If the degree of the dividend is 5 and the degree of the divisor is 3, then the degree of the quotient will be
On dividing f(x) = x3 – 3x2 + x + 2 by a polynomial g(x) the quotient and remainder q(x) and r(x) are (x – 2) and (-2x + 4) respectively, then g(x) is
The three zeroes of the polynomial 2x3 + 5x2 – 28x – 15 _____
If two of the zeroes of the polynomial f (x) = x4 – 3x3 – x2 + 9x – 6 are -√3 and √3 then all the zeroes are
If (x + 1) is a factor of 2x3 + ax2 + 2bx + 1, then find the values of a and b given that 2a – 3b = 4.
Which of the given is the set of zeroes of the polynomial p(x) = 2x3 + x2 – 5x + 2
The value of p when x3 + 9x2 + px – 10 is exactly divisible by (x+ 2) is ____
When the polynomial f(x) = 4x3 + 8x2 + 8x + 7 is divided by the polynomial g(x) = 2x2 – x + 1, the quotient and the remainder are
When x2 – 2x + k divides the polynomial x4 – 6x3 + 16x2 – 25x + 10, the remainder is (x + a). The value of a is _________
If the degree of the divisor g(x) is one then the degree of the remainder r(x) is
If the polynomial (2x + 3) is a factor of the polynomial 2x3 + 9x2 – x – b. The value of b is_______
If two of the zeros of the polynomial x4 – 17x3 + 90x2 – 166x + 92 are (7 + √3) and (7 – √3), then the other two zeros are _________
If f(x) is divided by g(x), g(x) ≠ 0, then there exist two polynomials q(x) and r(x) such that
The expression that should be added to the polynomial f(x) = x4 + 2x3 – 2x2 + x + 1, so that it should be exactly divisible by (x2 + 2x – 3) is
When x3 – 3x2 + 5x – 3 is divided by x2 – k , the remainder is 7x + a . Then the value of k is_____
If two zeroes of a polynomial 4x4 -20x3 +23 x2 + 5x – 6 are ½ and – ½, the how many more zeroes does it have?
|
461 tests
|