Mathematics: CUET Mock Test - 3 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 3
Bag 1 contains 4 white and 6 black balls while another Bag 2 contains 4 white and 3 black balls. One ball is drawn at random from one of the bags and it is found to be black. Find the probability that it was drawn from Bag 1.
The total revenue (in Rs.) received by selling 'x' units of a certain products is given by: R(x) = 4x2 + 10x + 3.
What is the marginal revenue on selling 20 such units?
If x is a real, then minimum value of x2 − 8x + 17 is:
If μ is mean of random variable X, with probability distribution
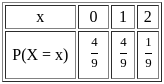
then value of 9μ + 4 is:
The Probability mass functions of Random variable X is:
P(X = x) = (0.6)x (0.4)1−x; x = 0, 1 The variance of X is:
Consider the following statements in respect of a function f(x):
1. f(x) is continuous at x = a, if limx→a f(x) exists.
2. If f(x) is continuous at a point, then 1/f(x) is also continuous at that point.
Which of the above statements is/are correct?
Determine the value of k, if  is continuous at x = 0
is continuous at x = 0
Consider the function
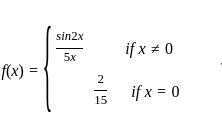
Which one of the following is correct in respect of the function?
Previous probabilities in Bayes Theorem that are changed with the new available information are called _____
Bag 1 contains 3 red and 5 black balls while another Bag 2 contains 4 red and 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it is drawn from bag 2.
_____ is the complement of the angle between the line L and a normal line to the plane π.
Find the angle between the planes x + 2y + 3z + 1 = 0 and (4, 1, -7).
What is the plane equation involved in the formula sinθ =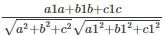 ?
?
What is the relation between the plane ax + by + cz + d = 0 and a1, b1, c1 the direction ratios of a line, if the plane and line are parallel to each other?
The condition a1a + b1b + c1c = 0 is for a plane and a line are _____ to each other.
Find the angle between 2x + 3y – 2z + 4 = 0 and (2, 1, 1).
The plane 5x + y + kz + 1 = 0 and directional ratios of a line (3, -1, 1) are parallel, find k.
Find k for the given plane x + 2y + kz + 2 = 0 and directional ratios of a line (8, 3, 2), if they are parallel to each other.
If θ is the angle between line whose ratios are a1, b1, c1 and the plane ax + by + cz + d = 0 then
cos θ = 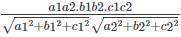
Which trigonometric function is used to find the angle between a line and a plane?
A plane and a line having an angle of 90 degrees between them are called _____
The condition a/a1 = b/b1 = c/c1 is for a plane and a line are _____ to each other.
Find the angle between x + 2y + 7z + 2 = 0 and (2, 4, 6).
Find the angle between the planes 5x + 2y + 3z + 1 = 0 and (1, 1, -2).
_____ is the angle between the normals to two planes.
What is the formula to find the angle between the planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0?
|
8 docs|148 tests
|



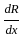
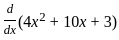

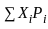 =
= 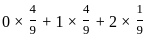 =
= 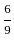
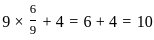
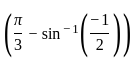 :
: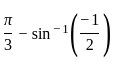
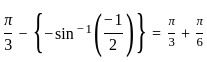
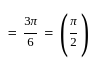
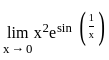 ?
?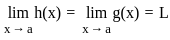 , then
, then 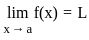 .
.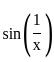 ≤ 1
≤ 1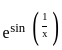 ≤ e1
≤ e1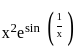 ≤ x2e
≤ x2e
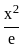 , f(x) =
, f(x) = 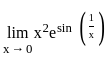 and g(x) = x2e.
and g(x) = x2e.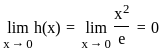 .
.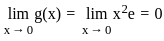 .
.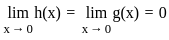 , we must have
, we must have 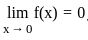 .
.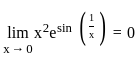 .
.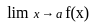 exists if
exists if 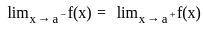
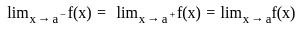
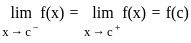
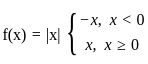
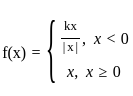 is continuous at x = 0
is continuous at x = 0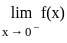
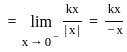 (∵ |x| = -x, for x < 0)
(∵ |x| = -x, for x < 0)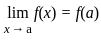 exists or its graph is a single unbroken curve.
exists or its graph is a single unbroken curve.


 .
.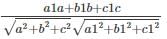
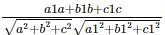
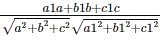
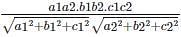
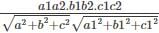 .
. .
.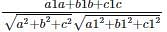 .
.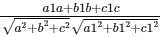 .
.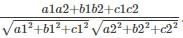 .
.











