Mathematics: CUET Mock Test - 5 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 5
Mr. Dev wishes to purchase an AC for Rs. 45, 000 with a down payment of Rs. 5000 and balance in EMI for 5 years. If Bank charges 6% per annum compounded monthly then monthly EMI is: 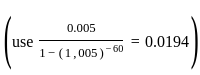
The cost of a machine is Rs. 20,000 and its estimated useful life is 10 years. The scrap value of the machine, when its value depriciates at 10% p.a, is:
use (0.9)10 = 0.35
Below are the stages for Drawing statistical inferences.
A. Sample
B. Population
C. Making Inference
D. Data tabulation
E. Data Analysis
Choose the correct answer from the options given below:
What is the length of the perpendicular drawn from point (3, 4, 5) to line 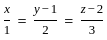 ?
?
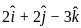 ?
?
If cosines of angles made by vector with coordinate axes are l, m and n then which option is correct?
What property this does this equation come under 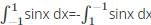
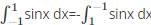 ?
?
What is the reverse integral property of definite integrals?
If the order of the matrix is m×n, then how many elements will there be in the matrix?
Does Rolle’s theorem applicable if f(a) is not equal to f(b)?
Another form of Rolle’s theorem for the continuous condition is _____
The matrix which follows the conditions m=n is called?
The matrix which follows the condition m>n is called as ____________
Function f should be _____ on [a,b] according to Rolle’s theorem.
What is the relation between f(a) and f(b) according to Rolle’s theorem?
|
39 docs|148 tests
|


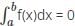 ?
? .
.
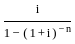
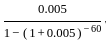
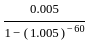

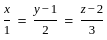 and point (3, 4, 5)
and point (3, 4, 5)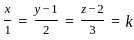
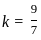
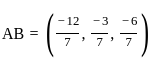

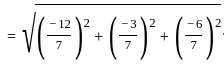
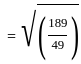
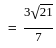
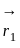 and parallel to the vector
and parallel to the vector  is given by:
is given by: 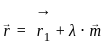
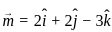
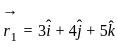
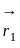 and parallel to the vector
and parallel to the vector  is given by:
is given by: 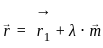
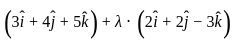
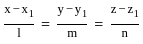
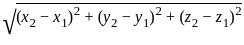
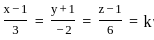 (let)
(let)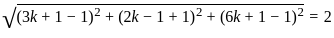
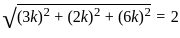
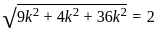
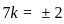
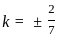
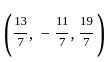 and
and 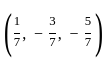
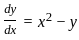 ?
?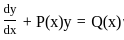 is given by
is given by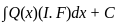
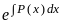
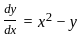 ⇒
⇒ 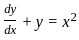
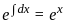
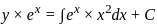
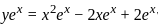
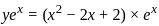
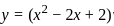
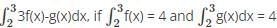 .
.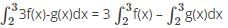
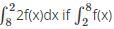 = -3.
= -3.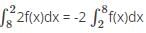
 = 2.
= 2.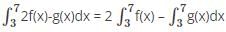
 .
.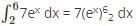
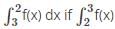 = 4.
= 4.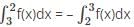
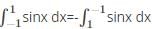 comes under the reverse integral property.
comes under the reverse integral property.
 ?
?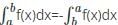 .
.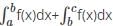 .
.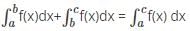
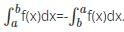
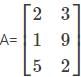 ?
?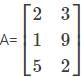 has 3 rows and 2 columns. Therefore, the order of the matrix is 3×2.
has 3 rows and 2 columns. Therefore, the order of the matrix is 3×2.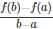 .
.











