Mathematics: CUET Mock Test - 7 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 7
(a,a) ∈ R, for every a ∈ A. This condition is for which of the following relations?
If Rs. x is the monthly increase in subscription amount, then the number of subscribers are
The number of subscribers which gives the maximum revenue is
What is increase in changes per subscriber that yields maximum revenue?
If A and B are two events such that P(A⋃B) = 5/6, P(A⋂B) = 1/3, P(B) = ½, then the events A and B are
If A, B, C are three mutually exclusive and exhaustive events such that if P(B) = 3/2 P(A) and P(C) = 1/2 P(B), then P(A) = _______
If A and B are two events such that P(A) ≠ 0 and P(A) ≠ 1, then 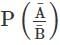
(a1, a2) ∈R implies that (a2, a1) ∈ R, for all a1, a2∈A. This condition is for which of the following relations?
Given a matrix A= 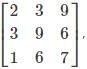 which of the elements aij follows the condition i=j.
which of the elements aij follows the condition i=j.
If f(x) = 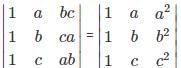 then which one among the following is correct?
then which one among the following is correct?
Which of the following is the formula for finding the area of a triangle with the vertices (x1,y1), (x2,y2), (x3,y3).
Which of the following is the formula for cofactor of an element aij?
If the system of equation 2x + 5y + 8z = 0, x + 4y + 7z = 0, 6x + 9y – αz = 0 has a non trivial solution then what is the value of α?
What is the area of the triangle whose vertices are (0,1), (0,2), (1,5)?
What is the minor of the element 5 in the determinant Δ= 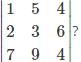
|
8 docs|148 tests
|



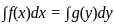
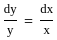
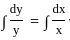
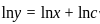

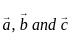 are coplanar, then what is
are coplanar, then what is  equal to?
equal to?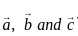 are coplanar if and only if [a b c] = 0
are coplanar if and only if [a b c] = 0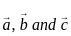 are coplanar i.e
are coplanar i.e 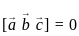
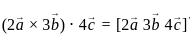 and
and 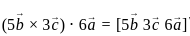
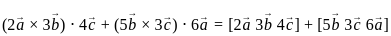
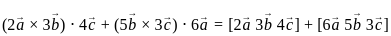
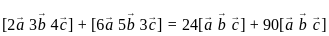
 are coplanar if and only if [a b c] = 0
are coplanar if and only if [a b c] = 0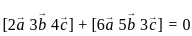
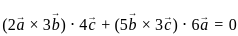
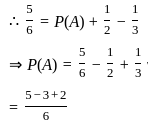
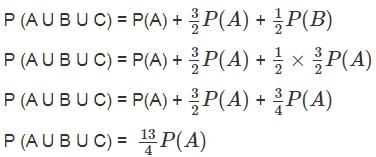
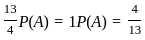
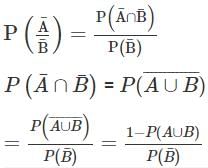
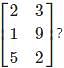
 has 3 rows and 2 columns. Therefore, the order of the matrix is 3×2.
has 3 rows and 2 columns. Therefore, the order of the matrix is 3×2.
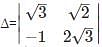
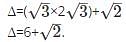
 are equal matrices.
are equal matrices.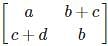 and
and 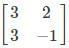 are equal matrices. Comparing the two matrices, we get a=3, b+c=2, c+d=3, b=-1
are equal matrices. Comparing the two matrices, we get a=3, b+c=2, c+d=3, b=-1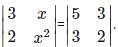
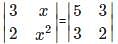

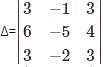


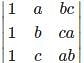
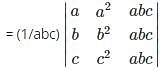
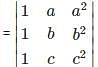
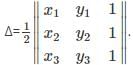

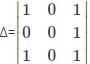
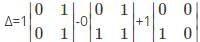

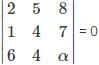
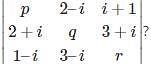

 is the determinant obtained by deleting the row and column containing element 5.
is the determinant obtained by deleting the row and column containing element 5.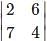 =2(4)-7(6)=-34.
=2(4)-7(6)=-34.
















