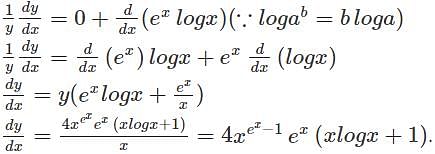Mathematics: CUET Mock Test - 8 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 8
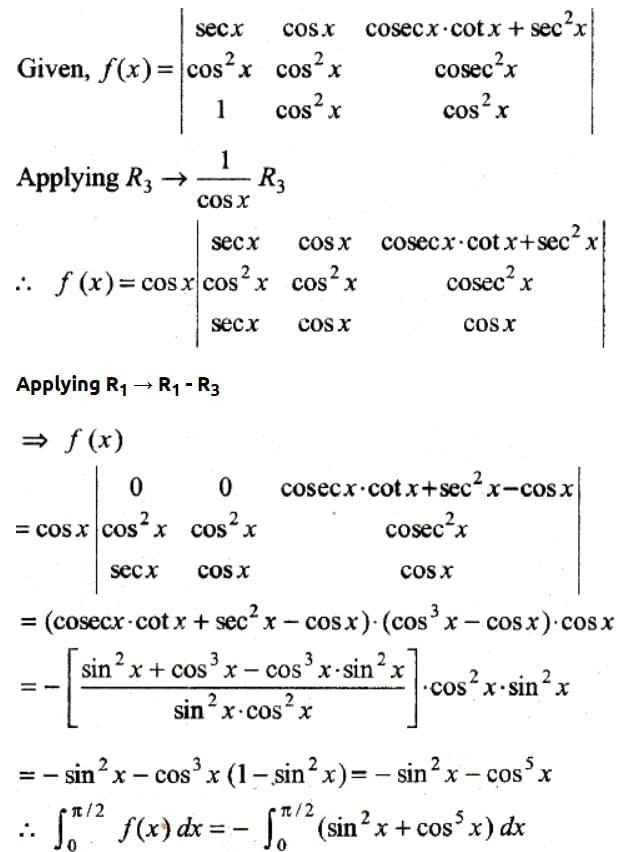
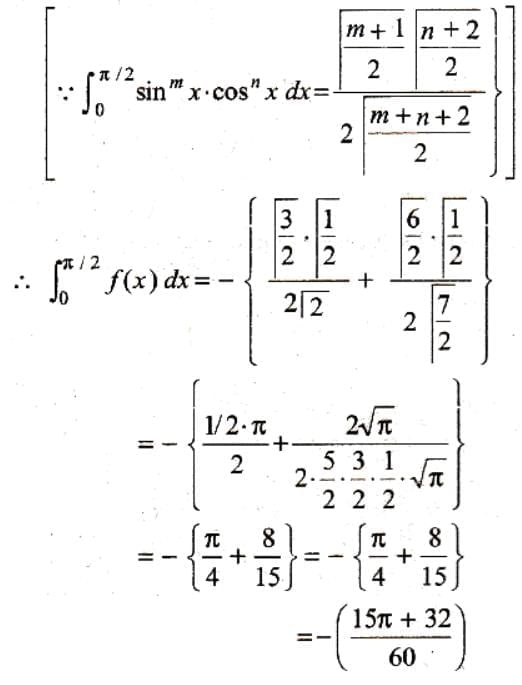
If f(x) = 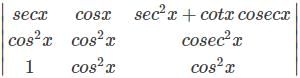 then what is the value of 0∫π/2 f(x) dx =
then what is the value of 0∫π/2 f(x) dx =
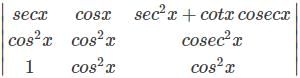 then what is the value of 0∫π/2 f(x) dx =
then what is the value of 0∫π/2 f(x) dx = Let A and B be two non zero square matrics and AB and BA both are defined. It means
If A = 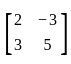 , then which of the following statements are correct?
, then which of the following statements are correct?
A. A is a square matrix
B. A−1 exists
C. A is a symmetric matrix
D. |A| = 19
E. A is a null matrix
Choose the correct answer from the options given below.
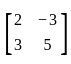 , then which of the following statements are correct?
, then which of the following statements are correct?Consider the matrix  . Which of the following is/are true?
. Which of the following is/are true?
The maximum value of the function f(x) = x3 − 3x2 + 2x in [1, 2] is:
Find the area of the triangle with the vertices (2,3), (4,1), (5,0).
For which of the elements in the determinant Δ= 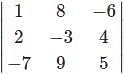 the cofactor is -37.
the cofactor is -37.
What is the relation between the two determinants f(x) = 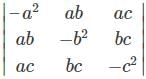 and g(x) =
and g(x) = 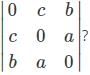
Find the equation of the line joining A(5,1), B(4,0) using determinants.
For which of the following elements in the determinant Δ= 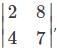 the minor of the element is 2?
the minor of the element is 2?
Find the value of k for which the points (3, 2), (1, 2), (5, k) are collinear.
For which of the following element in the determinant Δ= 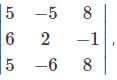 the minor and the cofactor both are zero.
the minor and the cofactor both are zero.
Which of the following conditions holds true for a system of equations to be consistent?
If the rate of change of radius of a circle is 6 cm/s then find the rate of change of area of the circle when r=2 cm.
A given systems of equations is said to be inconsistent if _____
|
8 docs|148 tests
|



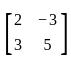 , we can see, the number of rows and columns are 2 respectively. Since the order of the matrix is 2 × 2, hence A is a square matrix.
, we can see, the number of rows and columns are 2 respectively. Since the order of the matrix is 2 × 2, hence A is a square matrix.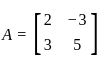
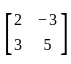 then AT =
then AT = 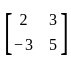
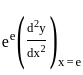 is:
is: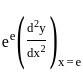 = 4 -1/e
= 4 -1/e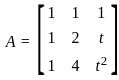 is invertible, we can analyze its determinant. A matrix is invertible if and only if its determinant is nonzero.
is invertible, we can analyze its determinant. A matrix is invertible if and only if its determinant is nonzero.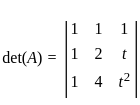
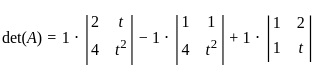
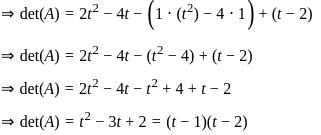
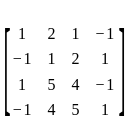 is
is
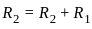

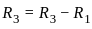
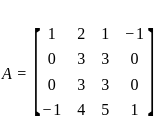
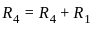
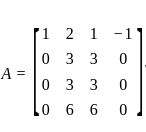
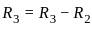
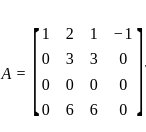
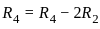
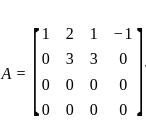
 = 0?
= 0?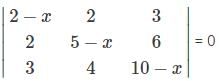
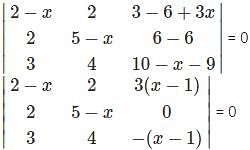
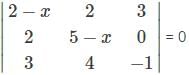
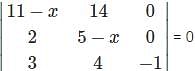

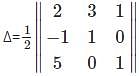
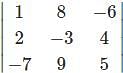
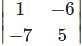 =1(5)-(-6)(-7)=5-42=-37
=1(5)-(-6)(-7)=5-42=-37 .
.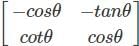
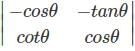
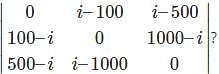
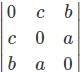
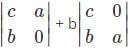
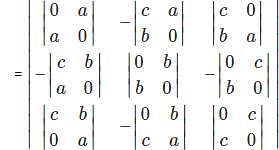
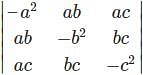
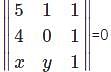
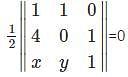
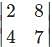

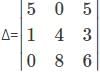
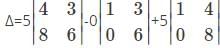
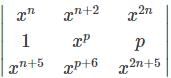 = 0,then what will be the value of p?
= 0,then what will be the value of p?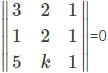
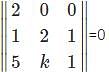
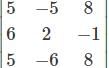
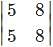 = 40-40 = 0
= 40-40 = 0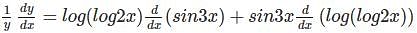
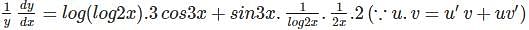
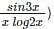
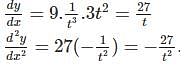
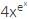 with respect to x.
with respect to x.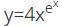
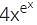
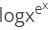 (∵logab =loga+logb)
(∵logab =loga+logb)