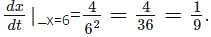Mathematics: CUET Mock Test - 9 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 9
Find the values of x and y for the given system of equations.
3x-2y=3
2x+2y=4
3x-2y=3
2x+2y=4
If 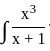 dx = q(x) − log|x + 1| + C then q(x) is equal to:
dx = q(x) − log|x + 1| + C then q(x) is equal to:
The solution of the differential equation xdy − ydx = 0 represent family of
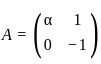 and
and 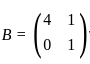 , such that A2 = B, then the value of α is:
, such that A2 = B, then the value of α is:
The total cost N(x) in rupees, associated with the production of x units of an item is given by N(x)=0.06x3-0.01x2+10x-43. Find the marginal cost when 5 units are produced.
The cost of 8kg apple and 3kg is Rs 70. The cost of 10kg apple and 6kg orange is 90. Find the cost of each item if x is the cost of apples per kg and y is the cost of oranges per kg.
The length of the rectangle is changing at a rate of 4 cm/s and the area is changing at the rate of 8 cm/s. What will be the rate of change of width if the length is 4cm and the width is 1 cm.
For a given system of equations if |A|=0 and (adj A)B≠O(zero matrix), then which of the following is correct regarding the solutions of the given equations?
Find the second order derivative of y=3x2 1 + log(4x)
For which of the values of x, the rate of increase of the function y=3x2-2x+7 is 4 times the rate of increase of x?
Find the value of x and y for the given system of equations.
3x+4y=6
5x-4y=4
The volume of a cube of edge x is increasing at a rate of 12 cm/s. Find the rate of change of edge of the cube when the edge is 6 cm.
|
8 docs|148 tests
|


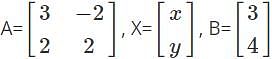
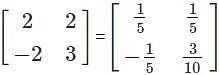

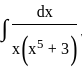 is equal to
is equal to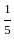
 =
= 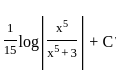

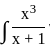 is simplified as
is simplified as 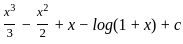 =
= 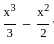
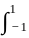 (|x − 2| + |x|) dx =
(|x − 2| + |x|) dx =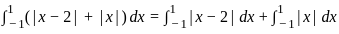
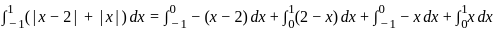
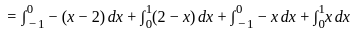
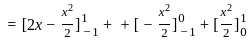
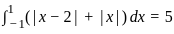
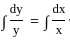
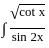 dx =
dx =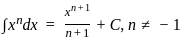
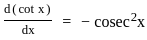
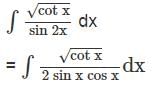
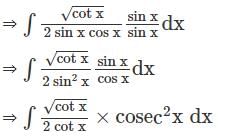
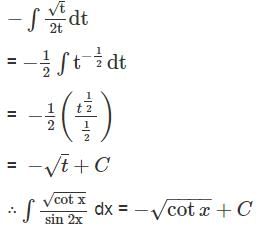
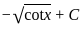 .
.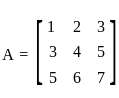 and
and 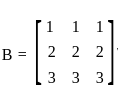 , then det(A + B) = ?
, then det(A + B) = ?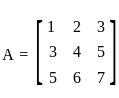 and
and 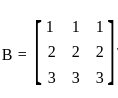
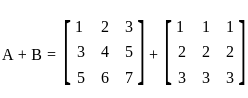
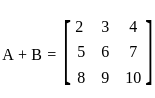
 is,
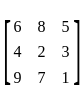
is,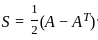 and K is the symmetric part which is given as
and K is the symmetric part which is given as 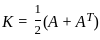 .
.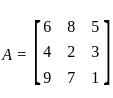
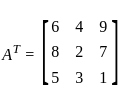

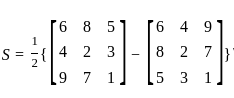
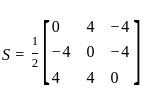
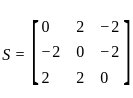
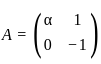 and
and 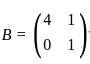 such that A
such that A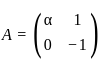 and
and 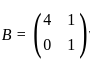
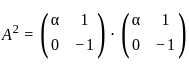
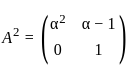
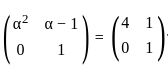
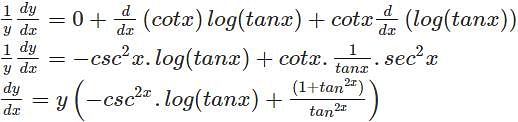
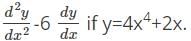
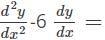 48x2−96x3−12
48x2−96x3−12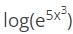 w.r.t x.
w.r.t x.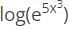
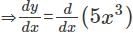
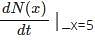 = 0.18(5)2-0.02(5)+10
= 0.18(5)2-0.02(5)+10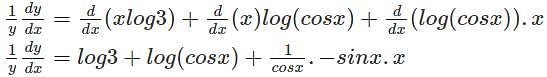
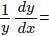 log3+log(cosx)-x tanx
log3+log(cosx)-x tanx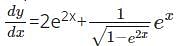
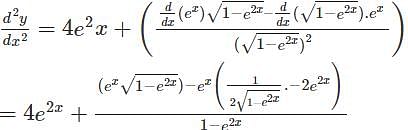
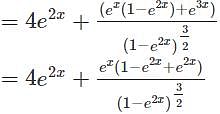
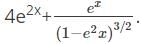
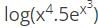 w.r.t x.
w.r.t x.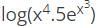
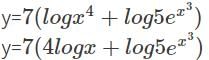
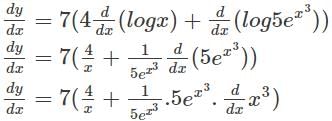
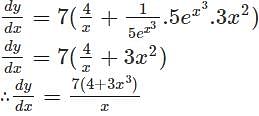
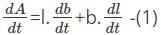
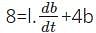
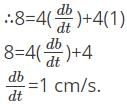
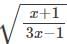 with respect to x.
with respect to x.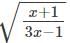
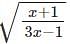
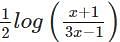
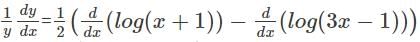
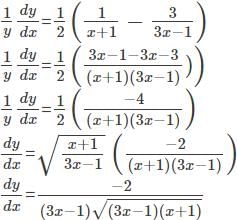
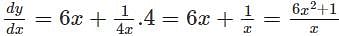


 logx w.r.t x.
logx w.r.t x.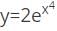 logx
logx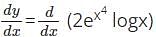
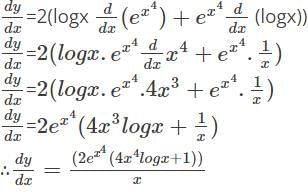
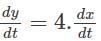

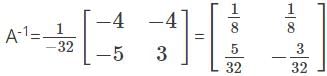

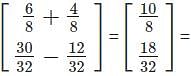

 with respect to x.
with respect to x.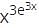
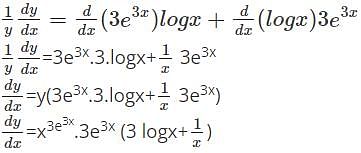

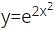
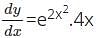
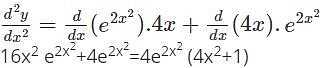
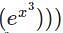 w.r.t x.
w.r.t x.