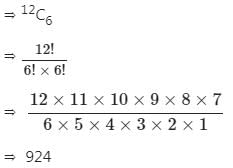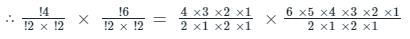MCQ: अनुक्रमण और संयोजन - 1 - Bank Exams MCQ
15 Questions MCQ Test Quantitative Aptitude/संख्यात्मक योग्यता - MCQ: अनुक्रमण और संयोजन - 1
5 लड़कियों और 3 लड़कों को एक पंक्ति में किस प्रकार बैठाया जा सकता है, ताकि कोई भी दो लड़के एक साथ न बैठें?
एक वॉलीबॉल टीम में 6 लोग होते हैं। 12 लोगों की एक कक्षा से टीम बनाने के कितने अलग-अलग तरीके हो सकते हैं?
8 पुरुषों और 10 महिलाओं में से 5 पुरुषों और 6 महिलाओं की एक समिति कितने तरीकों से बनाई जा सकती है?
शब्द 'GEOGRAPHY' के अक्षरों को कितने विभिन्न तरीकों से व्यवस्थित किया जा सकता है, ताकि स्वरों को हमेशा एक साथ रखा जा सके?
7 पुरुषों और 6 महिलाओं के समूह से, 5 व्यक्तियों का चयन करना है ताकि समिति में कम से कम 3 पुरुष हों। इसे कितने तरीकों से किया जा सकता है?
क्रिस्मस शब्द को कितने तरीकों से व्यवस्थित किया जा सकता है ताकि C और M कभी साथ न हों?
संख्याओं 2, 5, 6, 7 और 8 के साथ कितनी चार अंकों की संख्याएँ बनाई जा सकती हैं? (अंक दोहराए नहीं जा सकते)
4, 5, 2, 1, 8, 9 अंकों से कितनी अलग-अलग 6-अंकों की संख्याएँ बनाई जा सकती हैं?
3, 5 और 7 अंकों का उपयोग करके कितने संभावित दो-अंकीय नंबर बनाए जा सकते हैं (अंक दोहराए जा सकते हैं)?
5, 6, 7, 8, 9 अंकों से कितने 3 अंकीय विषम संख्याएँ बनाई जा सकती हैं, यदि अंकों को दोहराया जा सकता है।
शब्द 'FIGHT' के अक्षरों को कितने विभिन्न तरीकों से व्यवस्थित किया जा सकता है?
हम शब्द MANAGEMENT के अक्षरों को कितने तरीकों से क्रमबद्ध कर सकते हैं ताकि स्वर और व्यंजन की तुलनात्मक स्थिति MANAGEMENT में समान रहे?
चार कुर्सियों पर 10 व्यक्तियों के व्यवस्थाओं की संख्या -
8 भारतीयों, 4 अमेरिकियों और 4 अंग्रेजों को एक पंक्ति में कैसे बैठाया जा सकता है ताकि सभी लोग अपनी राष्ट्रीयता के अनुसार एक साथ बैठें?
|
223 docs|265 tests
|