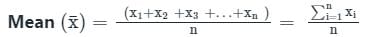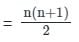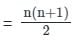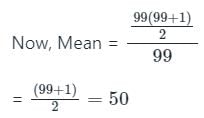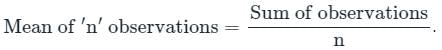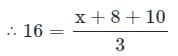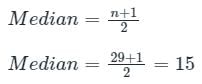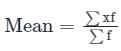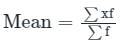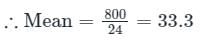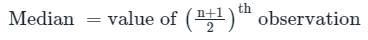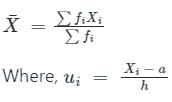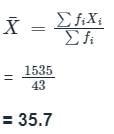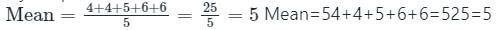MCQ: केंद्रीय प्रवृत्ति और परिवर्तन के माप - Bank Exams MCQ
15 Questions MCQ Test Quantitative Aptitude/संख्यात्मक योग्यता - MCQ: केंद्रीय प्रवृत्ति और परिवर्तन के माप
पहले 99 प्राकृतिक संख्याओं का औसत क्या है?
तीन संख्याओं का औसत 16 हो। यदि दो संख्याएँ 8 और 10 हैं, तो शेष संख्या क्या होगी?
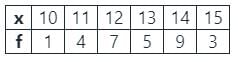
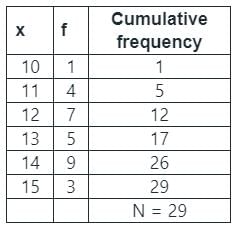
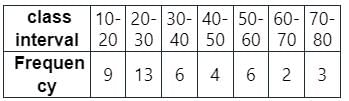
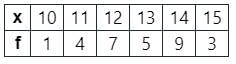
निम्नलिखित आवृत्ति वितरण का क्रमशः मोड और माध्यिका खोजें।

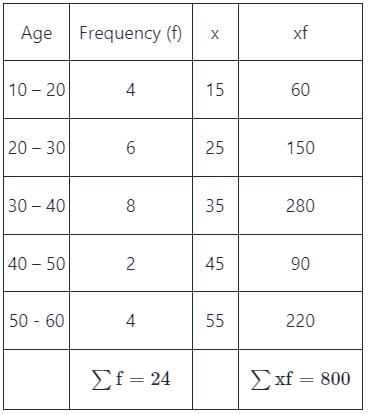
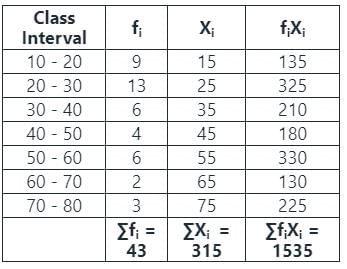
24 लोगों का एक यादृच्छिक नमूना उनकी उम्र के अनुसार निम्नलिखित तालिका में वर्गीकृत किया गया है:
इस समूह के लोगों की औसत आयु क्या है?

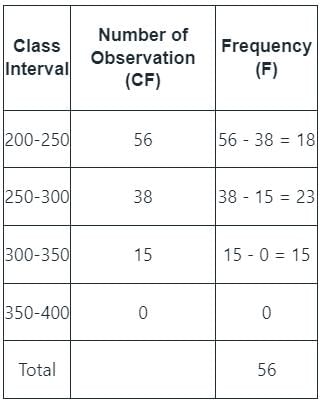
नीचे दिए गए डेटा से 250 और 300 के बीच अवलोकनों की संख्या खोजें: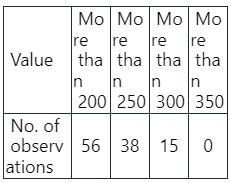
यदि निम्नलिखित डेटा का मोड 7 है, तो डेटा सेट 3, 8, 6, 7, 1, 6, 10, 6, 7, 2k + 5, 9, 7, और 13 में k का मान क्या होगा?
दिए गए संख्याओं के सेट का माध्य निकालें: 2, 6, 6, 8, 4, 2, 7, 9
यदि कुछ डेटा का औसत 4 और मोड़ 10 है, तो इसका माध्यिका क्या होगा?
नीचे दिए गए डेटा का रेंज, मोड और मीडियन का औसत क्या है?
5, 10, 3, 6, 4, 8, 9, 3, 15, 2, 9, 4, 19, 11, 4
20 संख्याओं का औसत शून्य है। इनमें से, अधिकतम, कितनी संख्या शून्य से अधिक हो सकती है?
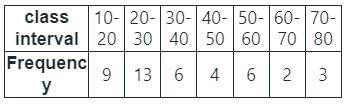
निम्नलिखित में से गणितीय माध्य का सही सूत्र कौन सा है?
जिस संख्या से छोटी ___________ अवलोकनों की संख्या उसी संख्या से बड़ी अवलोकनों की संख्या के समान होती है।
दी गई डेटा सेट के लिए: 4, 4, 5, 6, 6 निम्नलिखित में से कौन सा सत्य है?
कंपनी में 77 कर्मचारियों को दी गई औसत मासिक वेतन ₹78 थी। उनमें से 32 का औसत वेतन ₹45 था और अन्य 25 का ₹82 था। शेष का औसत वेतन क्या था?
|
223 docs|265 tests
|