JEE Advanced Level Test: Straight Lines- 1 - EmSAT Achieve MCQ
29 Questions MCQ Test Mathematics for EmSAT Achieve - JEE Advanced Level Test: Straight Lines- 1
If the magnitude of sum of two vectors is equal to the magnitude of difference of the two vectors, the angle between these vectors is
The ratio in which the line joining the points (3, –4) and (–5, 6) is divided by x-axis
The circumcentre of the triangle with vertices (0, 0), (3, 0) and (0, 4) is
The mid points of the sides of a triangle are (5, 0), (5, 12) and (0, 12), then orthocentre of this triangle is
Area of a triangle whose vertices are (a cos q, b sinq), (–a sin q, b cos q) and (–a cos q, –b sin q) is
The point A divides the join of the points (–5, 1) and (3, 5) in the ratio k : 1 and coordinates of points B and C are (1, 5) and (7, –2) respectively. If the area of ΔABC be 2 units, then k equals
If A(cosa, sina), B(sina, – cosa), C(1, 2) are the vertices of a ΔABC, then as a varies, the locus of its centroid is
The points with the co-ordinates (2a, 3a), (3b, 2b) & (c, c) are collinear
A stick of length 10 units rests against the floor and a wall of a room. If the stick begins to slide on the floor then the locus of its middle point is
The equation of the line cutting an intercept of 3 on negative y-axis and inclined at an angle tan-1(3/5) to the x-axis is
The equation of a straight line which passes through the point (–3, 5) such that the portion of it between the axes is divided by the point in the ratio 5 : 3 (reckoning from x-axis) will be
The equation of perpendicular bisector of the line segment joining the points (1, 2) and (–2, 0) is
Slope of a line is not defined if the line is
Coordinates of a point which is at 3 distance from point (1, –3) of line 2x + 3y + 7 = 0 is
Let P and Q be the points on the line joining A(–2 , 5) and B(3 , 1) such that AP = PQ = QB , then the mid point of PQ is
A line is perpendicular to 3x + y = 3 and passes through a point (2, 2). Its y intercept is
The equation of the line passing through the point (c, d) and parallel to the line ax + by + c = 0 is
The position of the point (8, –9) with respect to the lines 2x + 3y – 4 = 0 and 6x + 9y + 8 = 0 is
The line 3x + 2y = 6 will divide the quadrilateral formed y the lines x + y = 5, y – 2x = 8, 3y + 2x = 0 & 4y – x = 0 in
Locus of point of intersection of the perpendicular lines one belonging to (x + y – 2) + λ(2x + 3y – 5) = 0 and other to (2x + y – 11) + λ(x + 2y – 13) = 0 is a
If P(1, 0) ; Q(–1, 0) & R(2, 0) are three give points, then the locus of the points S satisfying the relation, SQ2 + SR2 = 2 SP2 is
The area of triangle formed by the lines x + y – 3 = 0, x – 3y + 9 = 0 and 3x – 2y + 1 = 0
The co-ordinates of foot of the perpendicular drawn on line 3x – 4y – 5 = 0 from the point (0, 5) is
The co-ordinates of the point of reflection of the origin (0, 0) in the line 4x – 2y – 5 = 0 is
The line (p + 2q)x + (p – 3q)y = p – q for different values of p and q passes through a fixed point whose co-ordinates are
Given the family of lines, a(3x+4y+6) + b(x+y+2) = 0. The line of the family situated at the greatest distance from the point P(2, 3) has equation
The base BC of a triangle ABC is bisected at the point (p, q) and the equation to the side AB & AC are px + qy = 1 & qx + py = 1. The equation of the median through A is
If the lines xsin2A + ysinA + 1 = 0, xsin2B + ysinB + 1 = 0, xsin2C + ysinC + 1 = 0 are concurrent where A, B, C are angles of triangle then ΔABC must be
The image of the pair of lines represented by ax2 + 2h xy + by2 = 0 by the line mirror y = 0 is
|
141 videos|213 docs|254 tests
|




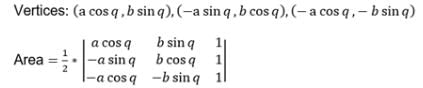
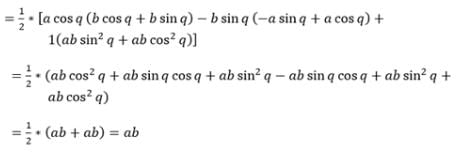


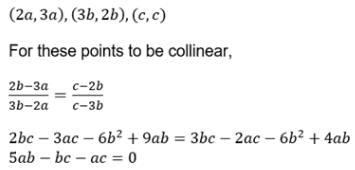


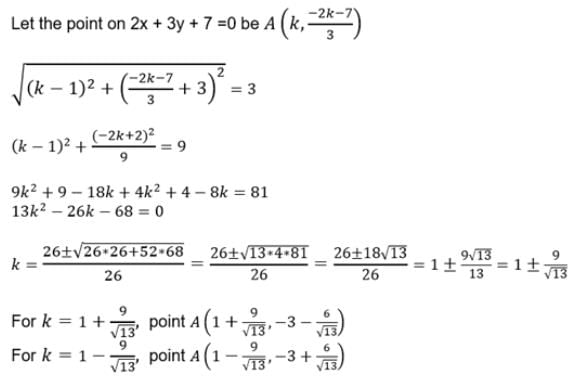
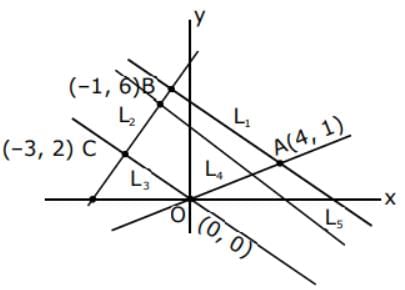 vertices of quadrilateral
vertices of quadrilateral