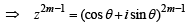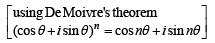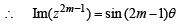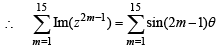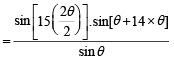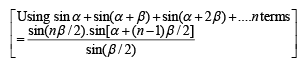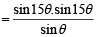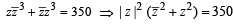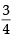JEE Advanced (Single Correct MCQs): Complex Numbers - JEE MCQ
30 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced (Single Correct MCQs): Complex Numbers
If the cube roots of unity are 1, ω, ω2, then the roots of the equation (x – 1)3 + 8 = 0 are (1979)
The smallest positive integer n for which (1980)
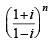 = 1 is
= 1 is
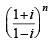 = 1 is
= 1 isThe complex numbers z = x+ iy which satisfy the equation 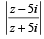 lie on....... (1981 - 2 Marks)
lie on....... (1981 - 2 Marks)
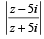 lie on....... (1981 - 2 Marks)
lie on....... (1981 - 2 Marks)The inequality |z – 4| < |z –2| represents the region given by (1982 - 2 Marks)
If z = x + iy and ω = (1 - iz) /( z - i) , then |ω|= 1 implies that, in the complex plane, (1983 - 1 Mark)
The points z1, z2, z3 z4 in the complex plane are the vertices of a parallelogram taken in order if and only if (1983 - 1 Mark)
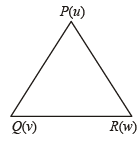
If a, b, c and u, v, w are complex numbers representing the vertices of two triangles such that c = (1 – r) a + rb and w = (1 – r)u + rv, where r is a complex number, then the two trian gles (1985 - 2 Marks)
If ω (≠1) is a cube root of unity and (1 + ω)7 = A + B ω then A and B are respectively (1995S)
Let z and ω be two non zero complex numbers such that |z| = |ω| and Arg z+ Arggω = π, then z equals (1995S)
Let z and ω be two complex numbers such that |z| ≤1, |ω| ≤ 1 and |z + iω| = | z – i 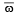 | = 2 then z equals (1995S)
| = 2 then z equals (1995S)
For positive integers n1, n2 the value of the expression (1 + i)n1 + (1 + i3)n1 + (1+ i5)n2 + (1+i7)n2 , where i = – 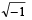 is a real number if and only if (1996 - 1 Marks)
is a real number if and only if (1996 - 1 Marks)
If i = 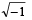 , then 4 + 5
, then 4 + 5 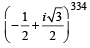 + 3
+ 3 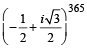 is equal to (1999 - 2 Marks)
is equal to (1999 - 2 Marks)
If arg(z) < 0, then arg (-z) - arg(z) = (2000S)
If z1, z2 and z3 are complex numbers such that (2000S)
|z1| = |z2| = |z3| = 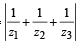 = 1, then |z1 +z2 +z3| is
= 1, then |z1 +z2 +z3| is
Let z1 an d z2 be nth roots of unity which subtend a right angle at the origin . Then n must be of the form (2001S)
The complex numbers z1, z2 and z3 satisfying 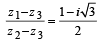 are the vertices of a triangle which is
are the vertices of a triangle which is
For all complex numbers z1, z2 satisfying |z1|=12 and | z2-3-4i| = 5, the minimum value of |z1-z2| is (2002S)
If |z| = 1 and ω = 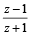 ( where Z ≠ 1) , then Re(ω) is
( where Z ≠ 1) , then Re(ω) is
If ω(≠1) be a cube root of unity and (1 + ω2)n = (1 + ω4)n, then the least positive value of n is (2004S)
The locus of z which lies in shaded region (excluding the boundaries) is best represented by (2005S)

a, b, c are integers, not all simultaneously equal and ω is cube root of unity (ω ≠ 1), then minimum value of |a + bω + cω2| is (2005S)
Let ω =-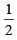 +i
+i 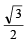 then the value of the det.
then the value of the det.
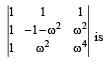 (2002 - 2 Marks)
(2002 - 2 Marks)
If 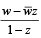 is purely real where w = α + iβ, β ≠ 0 and z ≠ 1,then the set of the values of z is (2006 - 3M, –1)
is purely real where w = α + iβ, β ≠ 0 and z ≠ 1,then the set of the values of z is (2006 - 3M, –1)
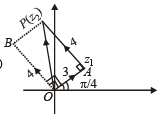
A man walks a distance of 3 units from the origin towards the north-east (N 45° E) direction. From there, he walks a distance of 4 units towards the north-west (N 45° W) direction to reach a point P. Then the position of P in the Argand plane is (2007 -3 marks)
If |z| = 1 and z ≠ ± 1, then all the values of 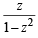 lie on (2007 -3 marks)
lie on (2007 -3 marks)
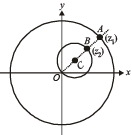
A particle P starts from the point z0 = 1 + 2i, where i = .It moves horizontally away from origin by 5 units and then vertically away from origin by 3 units to reach a point z1.From z1 the particle moves
.It moves horizontally away from origin by 5 units and then vertically away from origin by 3 units to reach a point z1.From z1 the particle moves 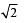 units in the direction of the vector
units in the direction of the vector 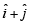 and then it moves through an angle
and then it moves through an angle 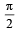 in anticlockwise direction on a circle with centre at origin, to reach a point z2. The point z2 is given by (2008)
in anticlockwise direction on a circle with centre at origin, to reach a point z2. The point z2 is given by (2008)
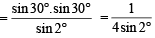
Let z = cosθ + i sinθ. Then the value of 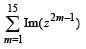
at θ = 2° is (2009)
Let z = x + iy be a complex number where x and y are integers.Then the area of the rectangle whose vertices are the roots of the equation : 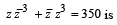 (2009)
(2009)
Let z be a complex number such that the imaginary part of z is non-zero and a = z2 + z + 1 is real. Then a cannot take the value
(2012)
|
446 docs|930 tests
|


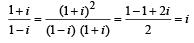

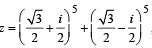 then (1982 - 2 Marks)
then (1982 - 2 Marks)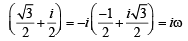
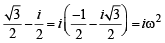
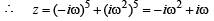
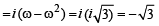
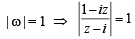
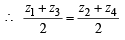 = z1+ z3 = z2+ z4
= z1+ z3 = z2+ z4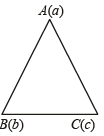
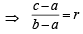 ....(1)
....(1)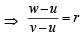 ....(2)
....(2)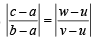 and
and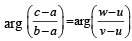
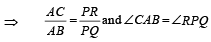

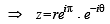

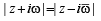
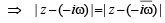
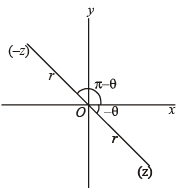
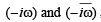 which is real ax is ,
which is real ax is , 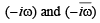 being mirror images of each other..
being mirror images of each other..
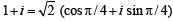
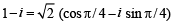
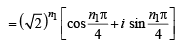
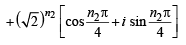

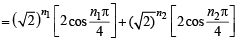
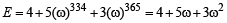
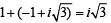
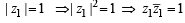
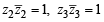
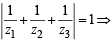
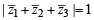
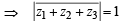 NOTE THIS STEP
NOTE THIS STEP
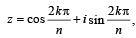 k, 0, 1, 2, .....,n -1.
k, 0, 1, 2, .....,n -1.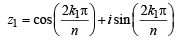
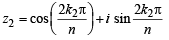
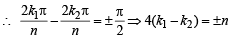
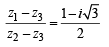
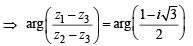
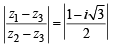
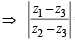
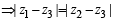
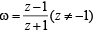
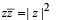
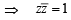 (for | z | = 1)
(for | z | = 1)
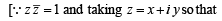
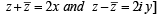
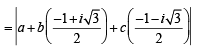
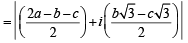
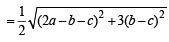
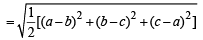
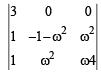
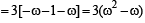
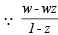 is purely real
is purely real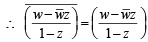
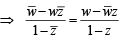
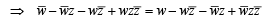
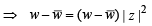
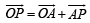
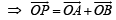
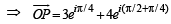
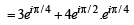
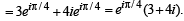
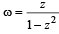
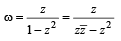
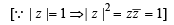
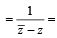 purely imaginary number
purely imaginary number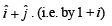
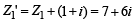
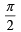 inanticlockwise direction, therefore Z2 = iZ1' = - 6+7i
inanticlockwise direction, therefore Z2 = iZ1' = - 6+7i