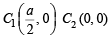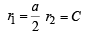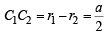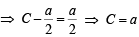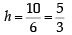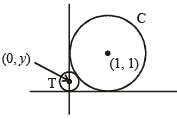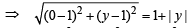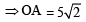Test: JEE Main 35 Year PYQs- Circle - JEE MCQ
29 Questions MCQ Test Additional Study Material for JEE - Test: JEE Main 35 Year PYQs- Circle
If the chord y = mx + 1 of the circle x2+y2=1 subtends an angle of measure 45° at the major segment of the circle then value of m is [2002]
The centres of a set of circles, each of radius 3, lie on the circle x2+y2=25. The locus of any point in the set is
The centre of the circle passing through (0, 0) and (1, 0) and touching the circle x2+y2=9 is [2002]
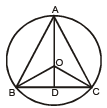
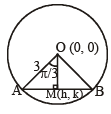
The equation of a circle with origin as a centre and passing through equilateral triangle whose median is of length 3a is
If the two circles ( x - 1)2 + ( y - 3)2 = r2 and x2 + y2 - 8 x + 2 y + 8 = 0 intersect in two distinct point, then[2003]
The lines 2 x - 3y=5 and 3x - 4 y = 7 are diameters of a circle having area as 154 sq.units.Then the equation of the circle is[2003]
If a circle passes through the point (a, b) and cuts the circle x2 + y2 = 4 orthogonally, then the locus of its centre is
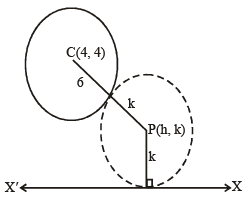
A variable circle passes through the fixed point A( p,q) and touches x-axis . The locus of the other end of the diameter through A is [2004]
If the lines 2x + 3 y + 1 = 0 and 3x -y - 4=0 lie alon g diameter of a circle of circumference 10p, then the equation of the circle is [2004]
Intercept on the line y = x by the circle x2 + y2 - 2x = 0 is AB. Equation of the circle on AB as a diameter is [2004]
If th e circles x2 + y2 + 2ax + cy + a = 0 and x2 + y2 – 3ax + dy – 1 = 0 intersect in two distinct points P and Q then the line 5x + by – a = 0 passes through P and Q for[2005]
A circle touches the x- axis and also touches the circle with centre at (0,3 ) and radius 2. The locus of the centre of the circle is[2005]
If a circle passes through the point (a, b) and cuts the circle x2 + y2 = p2 orthogonally, then the equation of the locus of its centre is [2005]
If the pair of lines ax2 + 2 (a + b)xy + by 2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then [2005]
If the lines 3x - 4y - 7=0 and 2x - 3y - 5=0 are two diameters of a circle of area 49π square units, the equation of the circle is [2006]
Let C be the circle with centre (0, 0) and radius 3 units. The equation of the locus of the mid points of the chords of the circle C that subtend an angle of 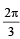 at its center is
at its center is
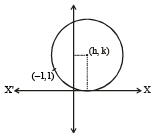
Consider a family of circles which are passing through the point (– 1, 1) and are tangent to x-axis. If (h, k) are the coordinate of the centre of the circles, then the set of values of k is given by the interval [2007]
The point diametrically opposite to the point P(1, 0) on the circle x2 + y2 + 2x + 4y – 3 = 0 is [2008]
The differential equation of the family of circles with fixed radius 5 units and centre on the line y = 2 is
If P an d Q are the points of intersection of the circles x2 + y2 + 3x + 7y+ 2p- 5 =0 and x2 + y2 + 2x + 2y – p2 = 0 then there is a circle passing through P, Q and (1, 1) for: [2009]
The circle x2 + y2 = 4x + 8y + 5 intersects the line 3x – 4y = m at two distinct points if [2010]
The two circles x2 + y2 = ax and x2 + y2 = c2 (c > 0) touch each other if [2011]
The length of the diameter of the circle which touches the x-axis at the point (1,0) and passes through the point (2,3) is: [2012]
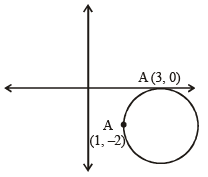
The circle passing through (1, –2) and touching the axis of x at (3, 0) also passes through the point [JEE M 2013]
Let C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to [JEE M 2014]
Locus of the image of the point (2, 3) in the line (2x – 3y + 4) + k (x – 2y + 3) = 0, k ∈ R, is a : [JEE M 2015]
The number of common tangents to the circles x2 + y2 – 4x – 6x – 12 = 0 and x2 + y2 + 6x + 18y + 26 = 0, is :[JEE M 2015]
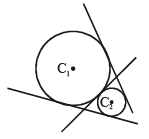
The centres of those circles which touch the circle, x2 + y2 – 8x – 8y – 4 = 0, externally and also touch the x-axis,lie on: [JEE M 2016]
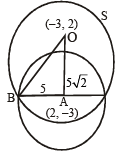
If one of the diameters of the circle, given by the equation, x2 + y2 – 4x + 6y – 12 = 0, is a chord of a circle S, whose centre is at (–3, 2), then the radius of S is: [JEE M 2016]
|
22 videos|162 docs|17 tests
|


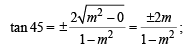
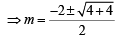
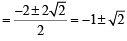
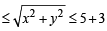

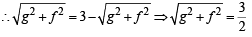
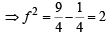
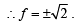

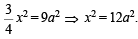
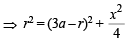
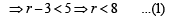

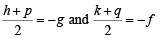
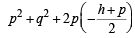
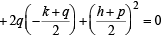
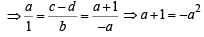
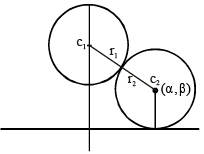
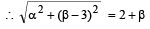
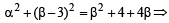
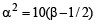
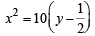 which is a parabola.
which is a parabola.
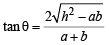
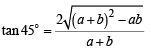

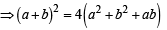
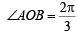
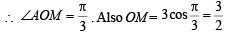
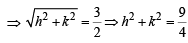
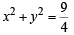
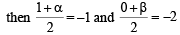
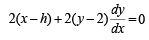
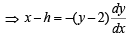
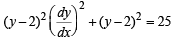
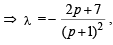 which does not exist for p = – 1
which does not exist for p = – 1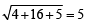
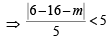 ⇒ |10 + m| < 25
⇒ |10 + m| < 25