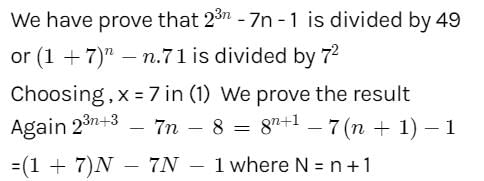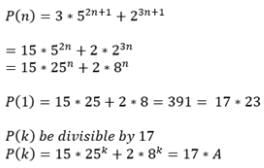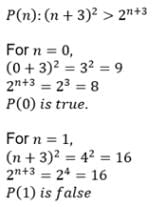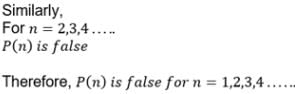Test: Principle Of Mathematical Induction- 2 - Commerce MCQ
25 Questions MCQ Test Online MCQ Tests for Commerce - Test: Principle Of Mathematical Induction- 2
If n is a +ve integer, then 33n−26n−1 is divisible by
If n is a +ve integer, then 23n−7n−1 is divisible by
If n is a +ve integer, then 3.52n+1+23n+1 is divisible by
If n is a +ve integer, then 72n−4 is divisible by
Let P (k) = 1 + 3 + 5 + …………….+ (2k – 1) = (3+k2).Then which of the following is true ?
The inequality 2n<n!,n∈N is true for :
For each n ∈ N,a2n−1+b2n−1 is divisible by :
For each n ∈ N, n (n + 1) (2n + 1) is divisible by :
For each n ∈ N, 3(52n+1)+23n+1 is divisible by :
For each n ∈ N, 23n−1 is divisible by :
For each n ∈ N, 32n−1 is divisible by :
The statement P (n) : “(n+3)2 > 2n+3 “ is true for :
The smallest positive integer ‘n‘ for which 2n(1×2×3×...............×n) < nn holds is :
If 10n+3×4n+1+k is divisible by 9 for all n ∈ N, then the least positive integral value of k is
The smallest positive integer n, for which ( 1 × 2 × 3 ×……×n )
Let P(n) : n2−n+41 is a prime number . then :
Let that P(n) ⇒ P(n+1) for all natural numbers n. also, if P (m) is true, m ∈ N, then we conclude that
Consider the statement P (n) : “n2 ≥ 100 “. Here P(n) ⇒ P(n+1) for all natural numbers n. Does it mean
The smallest positive integer ‘n‘ for which P (n) : 2n < (1×2×3×............×n) holds is :
If xn−1 is divisible by x – k for all n belongs to natural numbers N, then the least positive integral value of k is :
A student was asked to prove a statement P (n) by method of induction. He proved P (k + 1) is true whenever P (k) Is true for all k ≥ 5 , k ∈ N and P (5) is true. On the basis of this he could conclude that P (n) is true
If a,b,c ∈ N, an+bn is divisible by c, when n is odd but not when n is even, then the value of c is :
1.2.3 + 2.3.4 + 3.4.5 + ………..up to n terms is equal to :
The number of terms in the expansion of (x+y+z)n is
The sum of the terms in the nth bracket of the series 1 + (2+3+4) + (5+6+7+8+9) ….is
|
705 tests
|