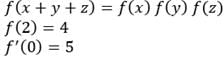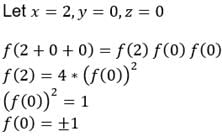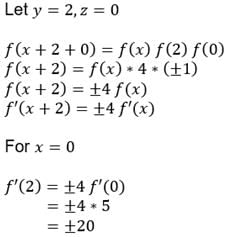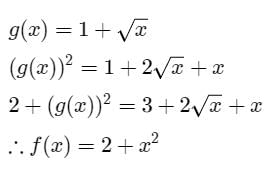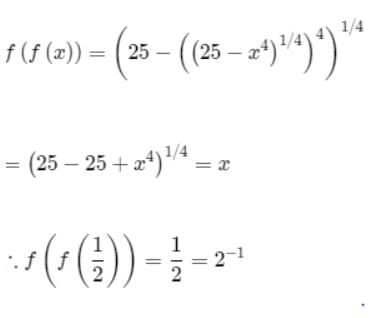Test: Relations & Functions- 4 - Commerce MCQ
25 Questions MCQ Test Online MCQ Tests for Commerce - Test: Relations & Functions- 4
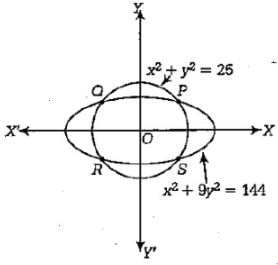
If A = {(x,y):x2+y2 = 25} and B = {(x,y) : x2+9y2+y2 = 144} then A∩B contains
The function f(x) = log (1+x/1-x) satisfies the equation
If f(x + y + z) = f(x) f(y) f(z) for all x , y z and if f(2) = 4, f’(0) = 5 and f(0) ≠ 0, then f’(2) is equal to
If A = {(x, y) : x2+y2 = 5} and B = {(x, y) : 2x = 5y}, then A∩B contains
If f : R → R is given by f(x) = |x| and A = {x∈R:x<0}, then f-1 (A) equals
If f : N × N →N is such that f (m, n) = m + n where N is the set of natural number, then which of the following is true ?
If A = [a, b], B = [c,d], C = [d, e] then {(a, c), (a, d), (a,e), (b,c), (b, d), (b, e)} is equal to
Suppose that g (x) = 1+ √x and f(g(x)) = 3 + 2 √x + x, then f (x) is
The number of elements in the Power set P(S) of the set S = [[Φ], 1, [2, 3]] is
If f(x) = (25 - x4)1/4 for 0 < x < √5, then f(f(1/2)) =
Two functions f:R→R g : R→Rare defined as follows :
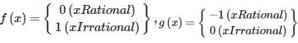
then (gof)(e) + (fog)(π) =
Let function f : R → R be defined by f(x) = 2x + sin x for x ∈ R. Then f is
|
705 tests
|