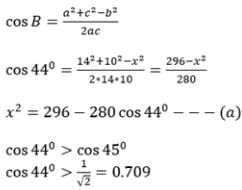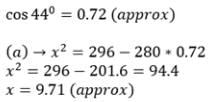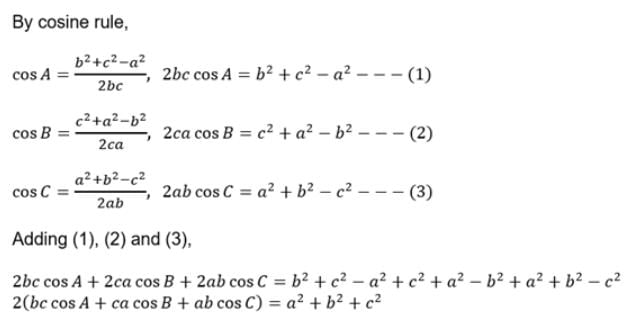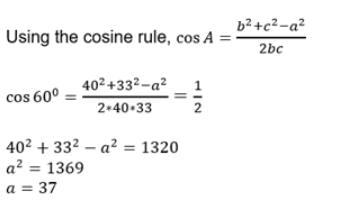JEE Exam > JEE Tests > Mathematics (Maths) for JEE Main & Advanced > Test: Solution of Triangles- Sine & Cosine Laws - JEE MCQ
Test: Solution of Triangles- Sine & Cosine Laws - JEE MCQ
Test Description
10 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Solution of Triangles- Sine & Cosine Laws
Test: Solution of Triangles- Sine & Cosine Laws for JEE 2025 is part of Mathematics (Maths) for JEE Main & Advanced preparation. The Test: Solution of Triangles- Sine & Cosine Laws questions and answers have been
prepared according to the JEE exam syllabus.The Test: Solution of Triangles- Sine & Cosine Laws MCQs are made for JEE 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Solution of Triangles- Sine & Cosine Laws below.
Solutions of Test: Solution of Triangles- Sine & Cosine Laws questions in English are available as part of our Mathematics (Maths) for JEE Main & Advanced for JEE & Test: Solution of Triangles- Sine & Cosine Laws solutions in
Hindi for Mathematics (Maths) for JEE Main & Advanced course. Download more important topics, notes, lectures and mock
test series for JEE Exam by signing up for free. Attempt Test: Solution of Triangles- Sine & Cosine Laws | 10 questions in 10 minutes | Mock test for JEE preparation | Free important questions MCQ to study Mathematics (Maths) for JEE Main & Advanced for JEE Exam | Download free PDF with solutions
Test: Solution of Triangles- Sine & Cosine Laws - Question 1
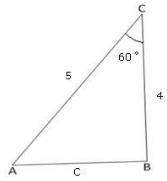
In the given figure,as per law of cosine which is the correct formula for a2
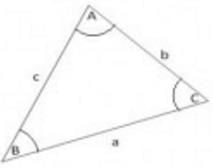

Detailed Solution for Test: Solution of Triangles- Sine & Cosine Laws - Question 1
Detailed Solution for Test: Solution of Triangles- Sine & Cosine Laws - Question 2
Test: Solution of Triangles- Sine & Cosine Laws - Question 3
Law of cosineis applicable if we know All three sides of triangle two angle and sides included All three angles All three sides of triangle two angle and sides included All three angles
Detailed Solution for Test: Solution of Triangles- Sine & Cosine Laws - Question 3
Detailed Solution for Test: Solution of Triangles- Sine & Cosine Laws - Question 4
Test: Solution of Triangles- Sine & Cosine Laws - Question 5
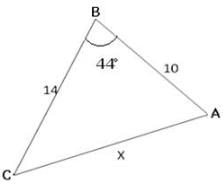
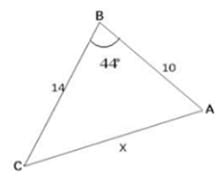
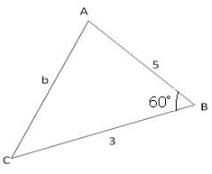
Find angle A in the following figure
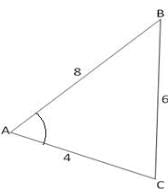
Detailed Solution for Test: Solution of Triangles- Sine & Cosine Laws - Question 5
Detailed Solution for Test: Solution of Triangles- Sine & Cosine Laws - Question 6
Detailed Solution for Test: Solution of Triangles- Sine & Cosine Laws - Question 7
Test: Solution of Triangles- Sine & Cosine Laws - Question 8
2(bc cos A+ ca cos B + ab cos C) =
Detailed Solution for Test: Solution of Triangles- Sine & Cosine Laws - Question 8
Test: Solution of Triangles- Sine & Cosine Laws - Question 10
Two ships A and B, lies 33 m apart on the sea surface. There is submarine ‘C’ on the sea bed. The angle of depression of C from A is 600 and the distance AC is 40 m. Calculate the distance BC.
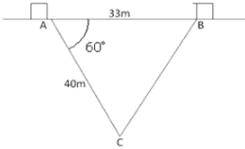
Detailed Solution for Test: Solution of Triangles- Sine & Cosine Laws - Question 10
|
209 videos|443 docs|143 tests
|
Information about Test: Solution of Triangles- Sine & Cosine Laws Page
In this test you can find the Exam questions for Test: Solution of Triangles- Sine & Cosine Laws solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Solution of Triangles- Sine & Cosine Laws, EduRev gives you an ample number of Online tests for practice
|
209 videos|443 docs|143 tests
|
Download as PDF