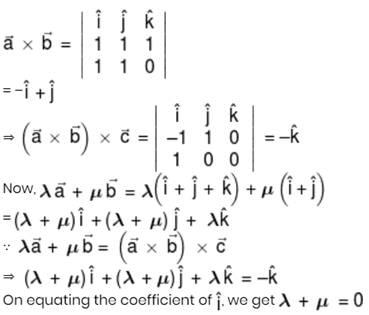JEE Main Maths Test- 7 - JEE MCQ
25 Questions MCQ Test - JEE Main Maths Test- 7
Let p and q be the position vectors of P and Qrespectively, with respect to O and |p| = p, |q| = q. The points R and S divide PQ internally and externally in the ratio 2:3 respectively. If 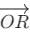 and
and 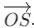 .
.
are perpendicular, then
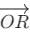 and
and 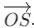 .
.are perpendicular, then
If the scalar product of the vector i + j + k with a unit vector parallel to the sum of vectors 2i + 4j – 5k and 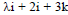 is equal to one, the λ is equal to
is equal to one, the λ is equal to
The unit vectors perpendicular to vectors i–j and i+j forming a right handed system is
If A = 2i+2j+3k, B = –i+ 2j+ k and C = 3i+ j, then A +t B is perpendicular to C if t is equal to
If the vectors a,b and c form the side BC,CA and AB respectively, of a triangle ABC, then
Let the vectors a,b,c and d be such that (a × b) × (c × d) = 0. Let P1 and P2 be planes determined by the pairs ofvectors a,b and c,d respectively. Then the angle between P1 and P2 is
If x and y are two unit vectors and is the angle between them, then
is equal to
If a and b are two unit vectors such that a+2b and 5a–4b are perpendicular to each other, then the angle between a and b is
Let a and b be two non-collinear unit vectors. if u = a – (a.b) b and v = a × b, then |v| is
If a.b and c are three non-coplanar vecotrs, then (a b c).[(a b)×(a c)] equals
If a, b and c are unit coplanar vectors, then the scalar triple product [2a–b 2b–c 2c–a] =
If a,b,c be three non-coplanar vectors, then the sum of
i. [a+b,b+c,c+a] =,
ii. [a–b,b–c,c–a] =
iii. [a×b,b×c,c×a] =
If a,b,c are non-coplanar unit vectors such that a (b and c non-coplanar) then the angle between a and b is
Let a, b and c be three vectors with magnitudes 1, 1 and 2 respectively. If a x (a x c) + b = 0, then the acute angle between a and c is?
The directional cosines of the line which is perpendicular to the lines with direction cosines proportional to 6,4,–4 and –6,2,1 is
Angle between the lines whose direction cosine are
given by l + m + n = 0, l2 + m2 – n2 = 0 is
The lines whose direction cosine are given by the relations a2l + b2m + c2n = 0 and mn + nl + lm = 0 are parallel if
The point of intersection of the line drawn form thevertices of any tetrahedran to the centroid of opposite faces divide the distance from each vertex to the opposite face in ratio
If vertices of tetrahedron are (1,2,3), (2,3,5),(3,–1,2) and (2,1,4) then its centroid is
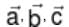 are three vectors of which every pair is non collinear. If the vector
are three vectors of which every pair is non collinear. If the vector 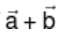 and
and 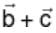 are collinear with
are collinear with  respectively then
respectively then 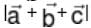 is :-
is :-
If a straight line make angles α, β, γ and δ with four diagonals of a cube, then the value of sin2 α + sin2 β + sin2 γ + sin2 δ is –
If the lines  intersect each other, then (λ + m) is equal to –
intersect each other, then (λ + m) is equal to –


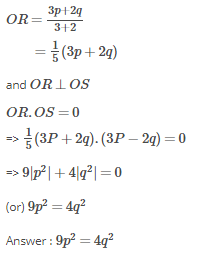
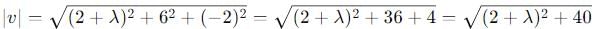
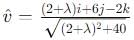
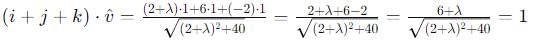
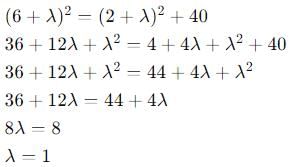

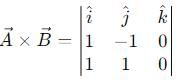
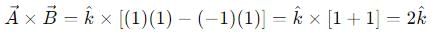
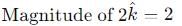

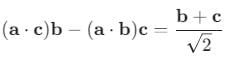
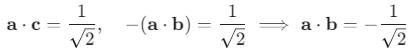
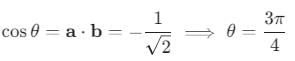
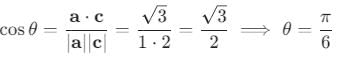
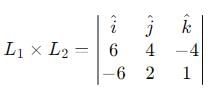
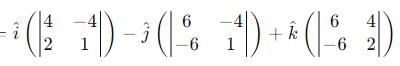
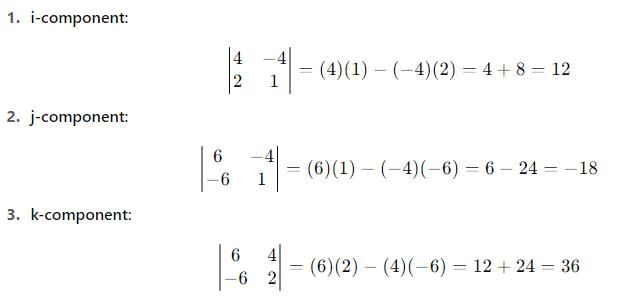
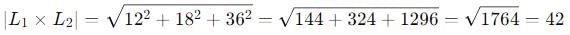
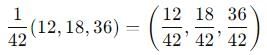
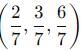
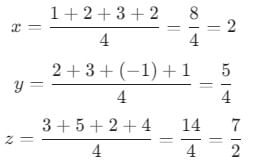
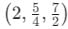
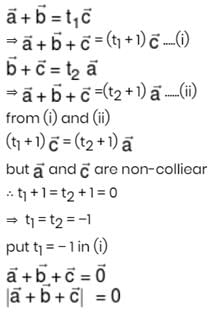
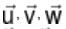 be vectors such that
be vectors such that  is :-
is :-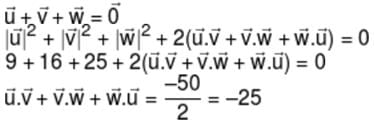
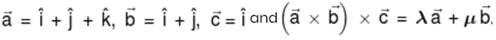 then λ + μ is equal to :-
then λ + μ is equal to :-