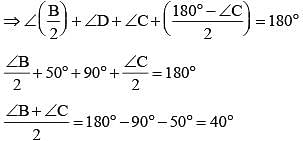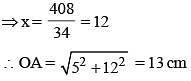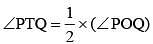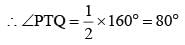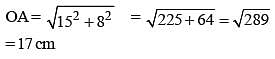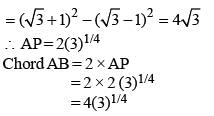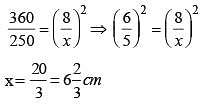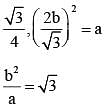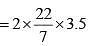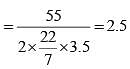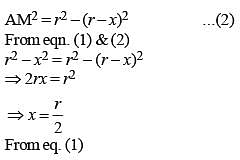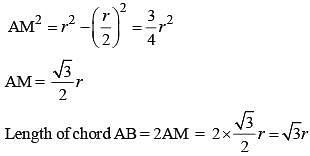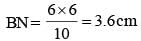SSC CGL Previous Year Questions: Geometry- 5 - SSC CGL MCQ
30 Questions MCQ Test SSC CGL Previous Year Papers - SSC CGL Previous Year Questions: Geometry- 5
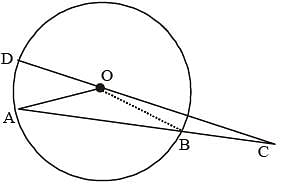
AB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting, AB produced at C such that BC = OD. If ∠BCD = 20°, then ∠AOD =? (SSC CGL 2nd Sit. 2013)
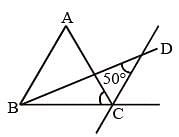
ABC is a triangle. The bisectors of the internal angle ∠B and external angle ∠C intersect at D. If ∠BDC = 50°, then ∠A is (SSC CGL 2nd Sit. 2013)
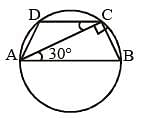
ABCD is a cyclic trapezium with AB || DC and AB = diameter of the circle. If ∠CAB = 30° then ∠ADC is (SSC CGL 2nd Sit. 2013)
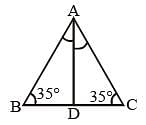
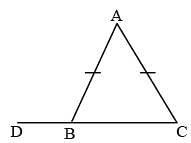
ABC is an isosceles triangle such that AB = AC and ∠B = 35°. AD is the median to the base BC. Then ∠BAD is: (SSC CGL 1st Sit. 2013)
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and distance between them is 17 cm, then the radius of the circle is: (SSC CGL 1st Sit. 2013)
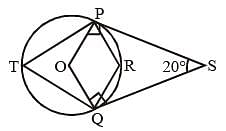
P and Q are two points on a circle with centre at O. R is a point on the minor arc of the circle, between the points P and Q. The tangents to the circle at the points P and Q meet each other at the point S. If ∠PSQ = 20°, ∠PRQ =? (SSC CGL 1st Sit. 2013)
If ABCD be a rectangle and P, Q, R, S be the mid points of  respectively, then the area of the quadrilateral PQRS is equal to: (SSC CGL 1st Sit. 2013)
respectively, then the area of the quadrilateral PQRS is equal to: (SSC CGL 1st Sit. 2013)
A chord of length 30 cm is at a distance of 8 cm from the centre of a circle. The radius of the circle is: (SSC CGL 1st Sit. 2013)
In a triangle ABC, AB = AC, ∠BAC = 40°. Then the external angle at B is: (SSC CGL 1st Sit. 2013)
A chord AB of a circle C1 of radius (√3 + 1) cm touches a circle C2 which is concentric to C1. If the radius of C2 is (√3 - 1) cm, the length of AB is: (SSC CGL 1st Sit. 2013)
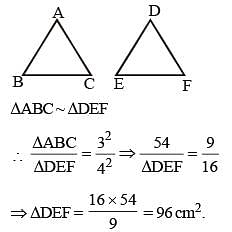
If ΔABC is similar to ΔDEF such that BC = 3 cm, EF = 4 cm and area of ΔABC = 54 cm2, then the area of ΔDEF is: (SSC CGL 1st Sit. 2013)
The perpendiculars, drawn from the vertices to the opposite sides of a triangle, meet at the point whose name is (SSC CHSL 2013)
If in ΔABC, ∠ABC = 5∠ACB and ∠BAC = 3 ∠ACB, then ∠ABC = (SSC CHSL 2013)
360 sq. cm and 250 sq. cm are the areas of two similar triangles. If the length of one of the sides of the first triangle be 8 cm, then the length of the corresponding side of the second triangle is (SSC CHSL 2013)
A chord 12 cm long is drawn in a circle of diameter 20 cm. The distance of the chord from the centre is (SSC CHSL 2013)
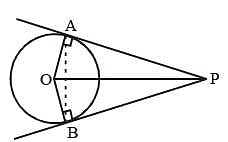
From a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then ∠APB is (SSC CHSL 2013)
In ΔABC. ∠A + ∠B = 145° and ∠C + 2∠B = 180°. State which one of the following relations is true? (SSC Sub. Ins. 2013)
In a triangle ABC, BC is produced to D so that CD = AC. If ∠BAD = 111° and ∠ACB = 80°, then the measure of ∠ABC is: (SSC Sub. Ins. 2013)
The areas of two similar triangles ABC and DEF are 20 cm2 and 45 cm2 respectively. If AB = 5 cm. then DE is equal to: (SSC Sub. Ins. 2013)
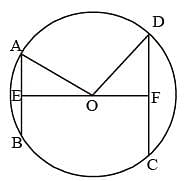
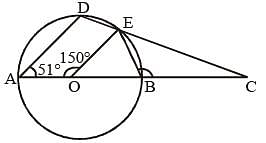
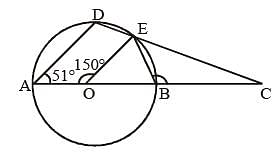
In the following figure. AB be diameter of a circle whose centre is O. If ∠AOE = 150°. ∠DAO = 51° then the measure of ∠CBE is: (SSC Sub. Ins. 2013)
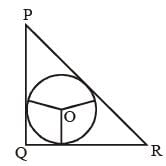
Triangle PQR circumscribes a circle with centre O and radius r cm such that ∠PQR = 90°. If PQ = 3 cm, QR= 4 cm, then the value of r is: (SSC Sub. Ins. 2013)
If area of an equilateral triangle is a and height b, then value of b2/a is: (SSC Sub. Ins. 2013)
A wheel rotates 3.5 times in one second. What time (in seconds) does the wheel take to rotate 55 radian of angle? (SSC CGL 2nd Sit. 2012)
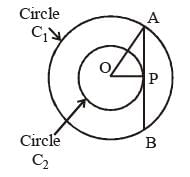
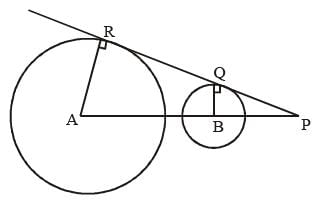
A and B are centres of the two circles whose radii are 5 cm and 2 cm respectively. The direct common tangents to the circles meet AB extended at P. Then P divides AB. (SSC CGL 2nd Sit. 2012)
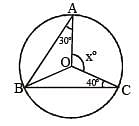
O is the centre of the circle passing through the points A, B and C such that ∠BAO = 30°, ∠BCO = 40° and ∠AOC = x°.
What is the value of x? (SSC CGL 2nd Sit. 2012)
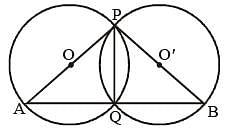
Two circles intersect each other at P and Q. PA and PB are two diameters. Then ∠AQB is (SSC CGL 2nd Sit. 2012)
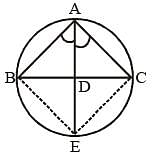
The bisector of ∠A of ΔABC cuts BC at D and the circumcircle of the triangle at E. Then (SSC CGL 2nd Sit. 2012)
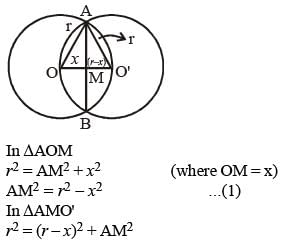
Two circles with same radius r intersect each other and one passes through the centre of the other. Then the length of the common chord is (SSC CGL 2nd Sit. 2012)
AB is a diameter of the circumcircle of ΔAPB; N is the foot of the perpendicular drawn from the point P on AB. If AP = 8 cm and BP = 6 cm, then the length of BN is (SSC CGL 2nd Sit. 2012)
If P, R, T are the area of a parallelogram, a rhombus and a triangle standing on the same base and between the same parallels lines which of the following is true? (SSC CGL 2nd Sit. 2012)
|
316 docs|268 tests
|