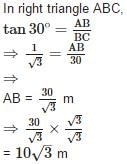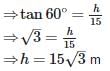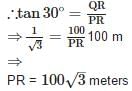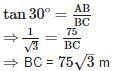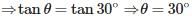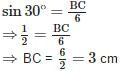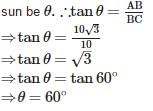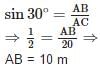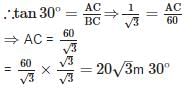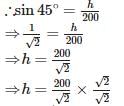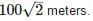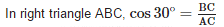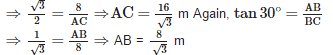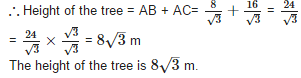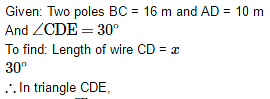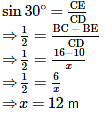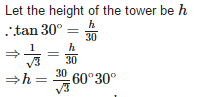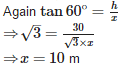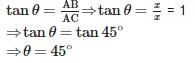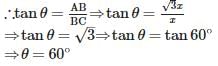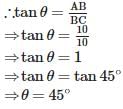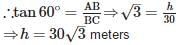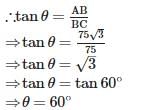RD Sharma Test: Some Applications of Trigonometry - Class 10 MCQ
25 Questions MCQ Test Mathematics (Maths) Class 10 - RD Sharma Test: Some Applications of Trigonometry
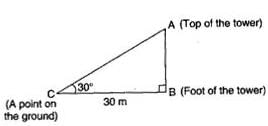
The angle of elevation of the top of a tower from a point on the ground and at a distance of 30m from its foot is 30°. The height of the tower is
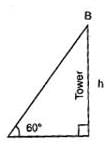
From a point on the ground which is 15m away from the foot of a tower, the angle of elevation is found to be 60°. The height of the tower is
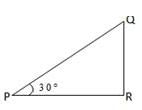
From a point P on the level ground, the angle of elevation of the top of a tower is 30°. If the tower is 100m high, the distance between P and the foot of the tower is
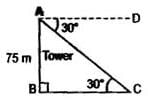
If the angle of depression of an object from a 75m high tower is 30°, then the distance of the object from the tower is
A ladder 14m long rests against a wall. If the foot of the ladder is 7m from the wall, then the angle of elevation is
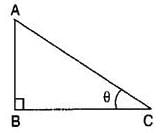
If the length of the shadow of a tower is √3 times that of its height, then the angle of elevation of the sun is
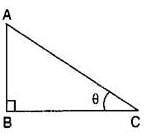
In a ΔABC right angled at B, ∠A = 30° and AC = 6cm, then the length of BC is
If a kite is flying at a height of 10√3m from the level ground attached to a string inclined at 60° to the horizontal then the length of the string is
The top of a broken tree has its top touching the ground at a distance of 10m from the bottom. If the angle made by the broken part with the ground is 30°, then the length of the broken part is
An electric pole is 10√3 m high and its shadow is 10m in length, then the angle of elevation of the sun is
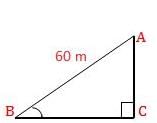
A kite is flying at a height of 60m from the level ground, attached to a string inclined at 30° to the horizontal. The length of the string is
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. If the angle made by the rope with the ground level is 30°, then the height of the pole is
A river is 60m wide. A tree of unknown height is on one bank. The angle of elevation of the top of the tree from the point exactly opposite to the foot of the tree, on the other bank, is 30°. The height of the tree is
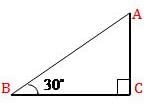
A bridge across a river makes an angle of 45° with the river bank. If the length of the bridge across the river is 200m, then the breadth of the river is
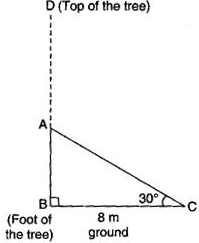
The upper part of a tree broken by the wind falls to the ground without being detached. The top of the broken part touches the ground at an angle of 30° at a point 8m from the foot of the tree. The original height of the tree is
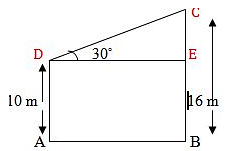
The tops of two poles of height 16m and 10m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is
If the shadow of a tower is 30m long, when the sun’s elevation is 30°. The length of the shadow, when the sun’s elevation is 60°is
If the angle of depression of a car from a 100m high tower is 45°, then the distance of the car from the tower is
If the length of the shadow of a tower is equal to its height, then the angle of elevation of the sun is
If the height of the tower is √3 times of the length of its shadow, then the angle of elevation of the sun is
A ladder 12m long rests against a wall. If it reaches the wall at a height of 6√3m, then the angle of elevation is
A pole 10m high cast a shadow 10m long on the ground, then the sun’s elevation is
If altitude of the sun is 60°, the height of a tower which casts a shadow of length 30m is
The measure of angle of elevation of the top of a tower 75√3m high from a point at a distance of 75m from the foot of the tower in a horizontal plane is
A person is flying a kite at a height of 30 m from the horizontal level. The length of string from the kite to the person is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite to the horizontal level is:
|
126 videos|457 docs|75 tests
|