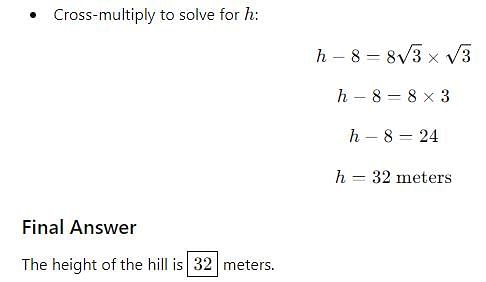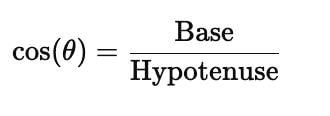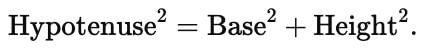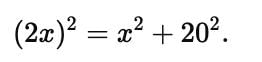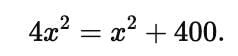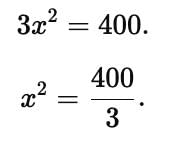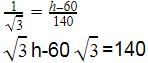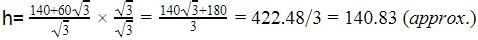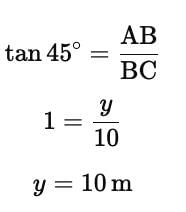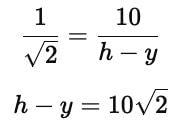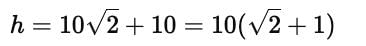Test: Applications of Heights & Distances - Class 10 MCQ
10 Questions MCQ Test Mathematics (Maths) Class 10 - Test: Applications of Heights & Distances
If the angles of depression from the top of a tower of height 40 m to the top and bottom of a tree are 45° and 60° respectively, then the height of the tree is
A man is standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and angle of depression of the base of the hill as 30°. What is the height of the hill?
A vertical tower is 20 m high. A man at some distance from the tower knows that the cosine of the angle of the elevation of the top of tower is 0.5. He is standing from the foot of the tower at a distance of:
A tower stands vertically on the ground. From a point on the ground 30 m away from the foot of the tower, the angle of elevation of the top of the tower is 45o. The height of the tower will be
The horizontal distance between two towers is 140 m. The angles of depression of the first tower, when seen from the top of the second tower is 30°. If the height of the first tower is 60 m. Find the height of the second tower.
A man is standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and angle of depression of the base of the hill as 30°. What is the height of the hill?
An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from his eyes is 45°. The height of the tower is
The shadow of a flag pole is 30 metres. If the altitude of the sun is at 30° then the height of the flag pole is
If the angle of elevation of a cloud from a point 100 metres above a lake is 30o and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
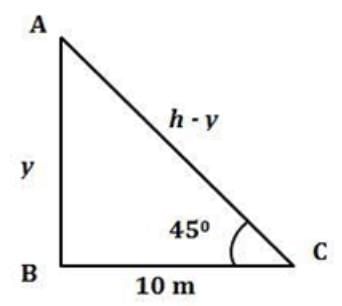
A tree is broken by wind and its upper part touches the ground at a point 10 metres from the foot of the tree and makes an angle of 45° with the ground. The entire length of the tree is
|
126 videos|457 docs|75 tests
|