Test: Spring - 2 - Mechanical Engineering MCQ
30 Questions MCQ Test GATE Mechanical (ME) Mock Test Series 2025 - Test: Spring - 2
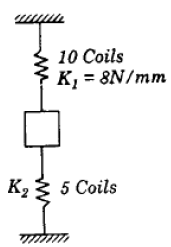
What is the equivalent stiffness (i.e. spring constant) of the system shown in the given figure?
A compression spring is made of music wire of 2 mm diameter having a shear strength and shear modulus of 800 MPa and 80 GPa respectively. The mean coil diameter is 20 mm, free length is 40 mm and the number of active coils is 10. If the mean coil diameter is reduced to 10 mm, the stiffness of the spring is approximately
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
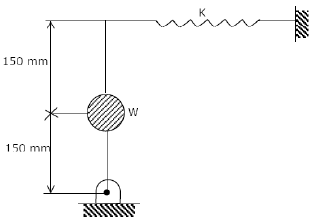
A uniform stiff rod of length 300 mm and having a weight of 300 N is pivoted at one end and connected to a spring at the other end. For keeping the rod vertical in a stable position the minimum value of spring constant K needed is:
The deflection of a spring with 20 active turns under a load of 1000 N is 10 mm. The spring is made into two pieces each of 10 active coils and placed in parallel under the same load. The deflection of this system is:
If both the mean coil diameter and wire diameter of a helical compression or tension spring be doubled, then the deflection of the spring close coiled under same applied load will
Assertion (A): Two concentric helical springs used to provide greater spring force are wound in opposite directions.
Reason (R): The winding in opposite directions in the case of helical springs prevents buckling.
A body having weight of 1000 N is dropped from a height of 10 cm over a close -coiled helical spring of stiffness 200 N/cm. The resulting deflection of spring is nearly
A closely-coiled helical spring is acted upon by an axial force. The maximum shear stress developed in the spring is t . Half of the length of the spring is cut off and the remaining spring is acted upon by the same axial force. The maximum shear stress in the spring the new condition will be:
A helical spring has N turns of coil of diameter D, and a second spring, made of same wire diameter and of same material, has N/2 turns of coil of diameter 2D. If the stiffness of the first spring is k, then the stiffness of the second spring will be :
Given that:
d = diameter of spring, R = mean radius of coils, n = number of coils and G = modulus of rigidity, the stiffness of the close-coiled helical spring subject to an axial load W is equal to
Which one of the following expresses the stress factor K used for design of closed coiled helical spring?
Where C = spring index
While calculating the stress induced in a closed coil helical spring, Wahl's factor must be considered to account for
Two helical springs of the same material and of equal circular cross-section and length and number of turns, but having radii 20 mm and 40 mm, kept concentrically (smaller radius spring within the larger radius spring), are compressed between two parallel planes with a load P. The inner spring will carry a load equal to
Two equal lengths of steel wires of the same diameter are made into two springs S1 and S2 of mean diameters 75 mm and 60 mm respectively. The stiffness ratio of S1 to S2 is
Wire diameter, mean coil diameter and number of turns of a closely-coiled steel spring are d, D and N respectively and stiffness of the spring is K. A second spring is made of same steel but with wire diameter, mean coil diameter and number of turns 2d, 2D and 2N respectively. The stiffness of the new spring is:
Consider the following statements:
When two springs of equal lengths are arranged to form a cluster spring
1. Angle of twist in both the springs will be equal
2. Deflection of both the springs will be equal
3. Load taken by each spring will be half the total load
4. Shear stress in each spring will be equal
Which of the above statements is/are correct?
When a weight of 100 N falls on a spring of stiffness 1 kN/m from a height of 2 m, the deflection caused in the first fall is:
When a helical compression spring is cut into two equal halves, the stiffness of each of the result in springs will be:
The equivalent spring stiffness for the system shown in the given figure (S is the spring stiffness of each of the three springs) is:
A mass is suspended at the bottom of two springs in series having stiffness 10 N/mm and 5 N/mm. The equivalent spring stiffness of the two springs is nearly
Two identical springs labelled as 1 and 2 are arranged in series and subjected to force F as shown in the given figure.
Assume that each spring constant is K. The strain energy stored in spring 1 is:
Assertion (A): Concentric cylindrical helical springs which are used to have greater spring force in a limited space is wound in opposite directions.
Reason (R): Winding in opposite directions prevents locking of the two coils in case of misalignment or buckling.
A close-coiled helical spring has wire diameter 10 mm and spring index 5. If the spring contains 10 turns, then the length of the spring wire would be:
Two close-coiled springs are subjected to the same axial force. If the second spring has four times the coil diameter, double the wire diameter and double the number of coils of the first spring, then the ratio of deflection of the second spring to that of the first will be:
The springs of a chest expander are 60 cm long when unstretched. Their stiffness is 10 N/mm. The work done in stretching them to 100 cm is:
A spring of stiffness 1000 N/m is stretched initially by 10 cm from the undeformed position. The work required to stretch it by another 10 cm is:
The length of the chest-expander spring when it is un-stretched, is 0.6 m and its stiffness is 10 N/mm. The work done in stretching it to 1m will be:
Two identical springs, each of stiffness K, are assembled as shown in the given figure. The combined stiffness of the assembly is:
The ends of the leaves of a semi-elliptical leaf spring are made triangular in plain in order to:
Consider the following types of stresses:
1. torsional shear 2. Transverse direct shear 3. Bending stress
The stresses, that are produced in the wire of a close-coiled helical spring subjected to an axial load, would include
|
29 docs|220 tests
|
|
29 docs|220 tests
|

















