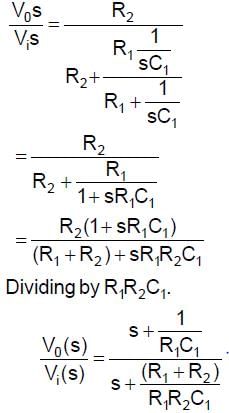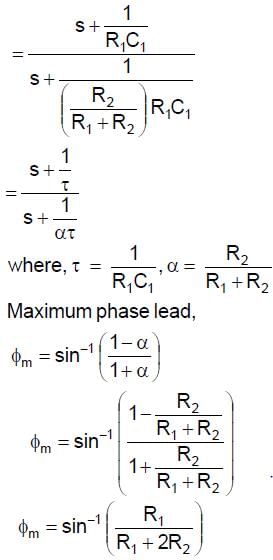Test: Control System - 1 - Electronics and Communication Engineering (ECE) MCQ
15 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Control System - 1
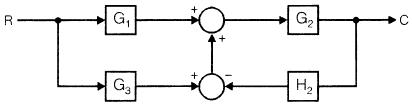
Determine C/R for the system given in figure below. Then put G3 = G1 G2 H2. Now the new
transfer function will be:
The unit impulse response of a system is h(t) = e-2t, t 0.
For this system, the steady-state value of the output for unit step input is equal to
A control system has input r(t) and output c(t). If the input is first passed through a block
whose transfer function is a-2s and then applied to the system, the modified output will be
The open-loop transfer function of a feedback control system is given by G(s)
Find the range of the values of T for stability.
If the open-loop transfer function of a feedback system is given by
G(s) H(s) = , then the controid of the asymptotes will be
For the block diagram shown in figure below, the limiting value of k for stability of the inner loop is found to be X < k < Y. The overall system will be stable if and only if
The closed loop transfer function of a control system has the following poles and zeros
Poles Zeros
P1 = 0.5 Z1 = –7
P2 = –1.0 Z2 = 9
P3 = –5
P4 = —10
The closed loop response can be closely approximated by considering which of the following?
Match List-I (Type of compensator) with List-II (Polar plot) and select the correct answer using the code given below the lists:
List-I
1.Phase lead
2. Phase lag
3. Lead-lag
A B C
(a)123
(b) 132
(c) 213
(d) 231
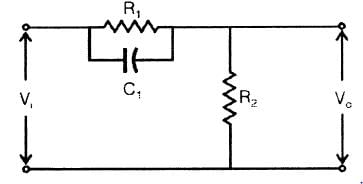
For the given network, the maximum phase lead 4m of Vo with respect to V1 is
In the Bode-plot of a unity feedback control system, the value of phase of G(j@) at the gain
cross-over frequency is —125°. The phase margin of the system is
The Nyquist plot for the function is
The condition for stability is given by
The open-loop transfer function of unity feedback system is G(s) = . Thes (s + 2) (s + 10)range of k for which closed-loop system is stable.
For the system shown below the state-space equation is X = A x + B u. The matrix A is
|
25 docs|263 tests
|