Test: Digital Communications - 2 - Electronics and Communication Engineering (ECE) MCQ
20 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Digital Communications - 2
The Autocorrelation function is given by exp 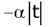 . Then the PSD is given by
. Then the PSD is given by
X is a binary memory less source with p (x = 0) = 0.3. If the source is transmitted over a BSC with cross-over probability = 0.1, then the capacity of the channel is
Two binary random variables X and Y are distributed according to the joint distributions p(x = y = 0) = p(x = 0, y = 1) = p(x = y = 1) = 1/3 . Then the entropy
H(x) is
In a Binary digital communication system, the threshold voltage of comparator is 'x' volts and voltage at input of comparator is uniformly distributed in the range of x-0.5 to x+0.25 when '0' is transmitted and it is in the range x-0.25 to x+0.5 when bit '1' is transmitted, the average probability of error in the system is_____________
If probability of error of PSK signal is 'x', then what will be probability of error of FSK and ASK signal. (Assume x =
If input to matched filter is s(t) = f(t)+ 2f (t)δ(t - 0.5) + f(t - 2.5)*8δ(t+ 0.5)
where f(t) is shown below, then determine the impulse response of matched filter h(t) ; 2 5 ≤ t < 3
(Note: δ is Delta function and * is convolution operator)
Match the following:
Modulation Type of signaling format to be
technique used for modulation
-
ASK (a) ON-OFF
-
PSK (b) Non return to zero
-
FSK (c) Return to zero
-
DPSK
-
QPSK
Consider a BSC with cross-over probability of error P. Suppose that R is the number of bits in a source code word that represents one of 2R possible levels at the output of quantizer. If R = 5, P = 0.01, then the probability of having 5 or less bits in error in a code word is_____________
A black and white television picture may be viewed as consisting of approximately 3x105 elements, each of which may occur one of 10 distinct brightness levels with equal probability. Transmission rate is 30 picture frames/ second and SNR is 30 dB. Then the minimum bandwidth required to support the transmission of the resulting video signal is MHz
A random variable X has
Q. The value of constant K is
A random variable X has
Q. The value of P(4 < x 5 ≤ 8) is
A telegraphic source has two symbols dot and dash. The dot duration is 0.2sec. The dash is twice as long as the dot and half as probable.
Q. The entropy of source is
A telegraphic source has two symbols dot and dash. The dot duration is 0.2sec. The dash is twice as long as the dot and half as probable.
Q. The information rate is
Consider a cascaded block of an LTI system
The impulse response of S1. is h1. t = δ t -2 The impulse response of 52 is h2 t = t.e-ru t
The input x(t) is wide sense stationary random process with Rxx 0 = 3 and variance = 1
Q. The mean of the random process w(t) is
Consider a cascaded block of an LTI system
The impulse response of S1. is h1. t = δ t -2 The impulse response of 52 is h2 t = t.e-ru t
The input x(t) is wide sense stationary random process with Rxx 0 = 3 and variance = 1
Q. If w(t) is input to system 52, then mean of process Y(t) will be
CDF of a random variable x is given below.
Q. E[x] is
CDF of a random variable x is given below.
Q. Variance is
Consider a discrete memory less source X with two symbols x1 and x2 and P (xi) = 0.9, P (x2) = 0.1. These symbols are encoded as below.
Q. Find the source efficiency η
Consider a discrete memory less source X with two symbols x1 and x2 and P (xi) = 0.9, P (x2) = 0.1. These symbols are encoded as below.
Q. Find the redundancy γ
The input to a linear delta modulator having a step-size D = 0.628 is a sine wave with frequency fm and peak amplitude Em. If the sampling frequency fs = 40kHz, the combination of the sine-wave frequency and peak amp, where slope overload will take place is
Em fin Em fin
(a) 0.3V 8kHz (b) 1.5V 4kHz
(c) 1.5V 2kHz (d) 3.0V 1kHz
|
25 docs|263 tests
|




















