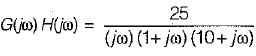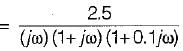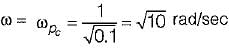Test: Frequency Domain Analysis of Control Systems- 2 - Electrical Engineering (EE) MCQ
20 Questions MCQ Test GATE Electrical Engineering (EE) Mock Test Series 2025 - Test: Frequency Domain Analysis of Control Systems- 2
If the bandwidth of the system is increased, then
Polar plot of G(s) = 1/(1+Ts) is a
Consider the following statements related to frequency domain analysis:
1. The cut-off rate is the slope of the log magnitude curve near the cut-off frequency.
2. The bandwidth is defined as the band of frequencies lying between 3 dB points.
3. Higher the value of resonant frequency of the system, slower is the time response.
4. The magnitude of resonant peak gives the information about the relative stability of the system.
Which of these statements is/are not correct?
1. The cut-off rate is the slope of the log magnitude curve near the cut-off frequency.
2. The bandwidth is defined as the band of frequencies lying between 3 dB points.
3. Higher the value of resonant frequency of the system, slower is the time response.
4. The magnitude of resonant peak gives the information about the relative stability of the system.
Which of these statements is/are not correct?
The inverse polar plot of the open loop transfer function, G(s) = (1+sT)/(sT) will be re presented by
The constant M-circles corresponding to the magnitude (M) of the closed loop transfer function of a linear system for value of M less than one lie in the G-plane and to the
The slope of the line due to 1/(jω)2 factor in magnitude part of Bode plot is
The magnitude plot of the open loop transfer function G(s) of a certain system is shown in figure below.
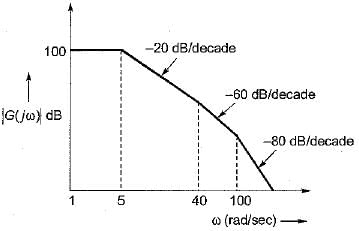
If the system is of minimum phase type, then the open-loop transfer function G(s) will be given by:
A unity feedback system has the open loop transfer function,
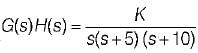
For the given system to be marginally stable, the value of gain cross-over frequency would be
The transfer function of a lag-lead network is given by
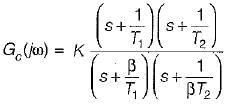
The phase of Gc (jω) will become zero at
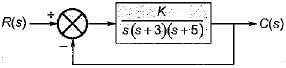
For the system shown below, what is the range of value of K for stability?
Match List-I (Polar plot of systems) with List-ll (Transfer functions) and select the correct answer using the codes given below the lists:
List-I
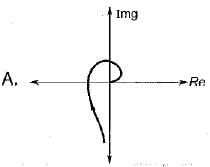
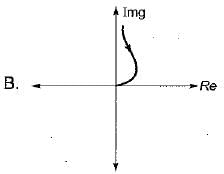
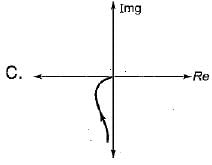
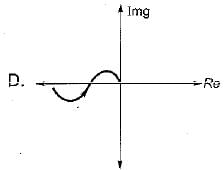
List-II
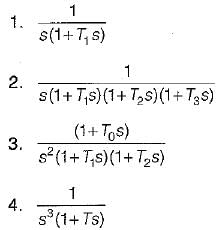
Codes:
A B C D
(a) 3 1 2 4
(b) 2 4 1 3
(c) 2 1 4 3
(d) 1 2 3 4
Assertion (A): The Nyquist criterion represents a method of determining the location of the characteristic equation roots with respect to the left half and the right half of the s-plane.
Reason (R): The Nyquist criterion does not give the exact location of the characteristic equation roots.
Which of the following is not true?
If the Nyquist plot cuts the negative real axis at a distance of 0.25, then the gain margin and phase margin of the system will be respectively
Match List-I (Different values of damping ratio) with List-II (Values of resonant peaks) and select the correct answer using the codes given below the lists:
List-I
A. ξ = 0
B. ξ = 0.707
C. ξ = 0.85
D. ξ = 0.5
List-II
1. More than unity
2. Not defined
3. Unity
4. infinite
Codes:
A B C D
(a) 1 3 2 4
(b) 4 1 2 3
(c) 4 3 2 1
(d) 1 2 3 4
Assertion (A) : Gain margin alone is adequate to indicate relative stability when system parameters other than the loop gain are subject to variation.
Reason (R) : Gain margin is the amount of gain in dB that can be added to the loop before the closed-loop system becomes unstable.
Assertion (A): Phase margin is measured at the gain crossover frequency.
Reason (R): Gain crossover frequency can be easily determined from Bode plot than from the Nyquist plot.
If the magnitude of closed loop transfer function of a system is given by M, then the centre and radius of M-circle will be respectively given by:
The open loop transfer function of a unity feedback system is given by
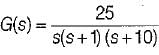
The value of ωpc, is
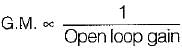
If the gain of the open-loop system is increased to four times, the gain margin of the system
|
25 docs|247 tests
|
|
25 docs|247 tests
|


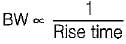
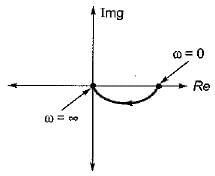

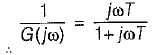
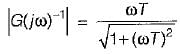

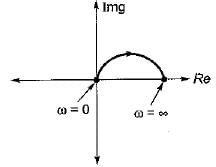
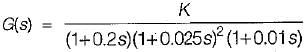
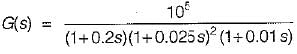
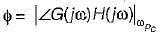
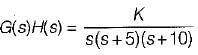
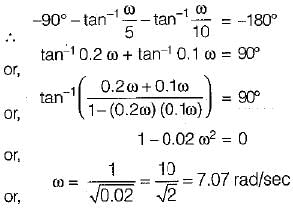
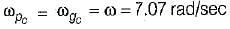
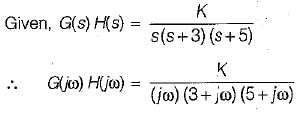
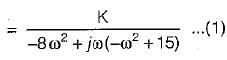
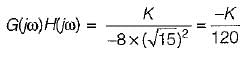
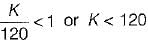
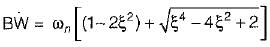 Thus,
Thus,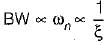
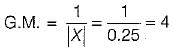
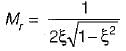
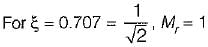
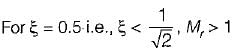
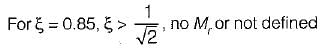
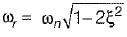
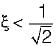 Hence for
Hence for 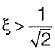 there is no Mr or M
there is no Mr or M