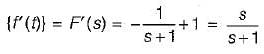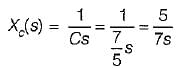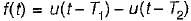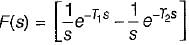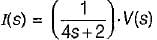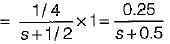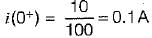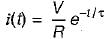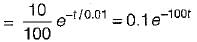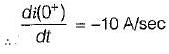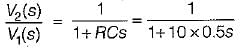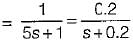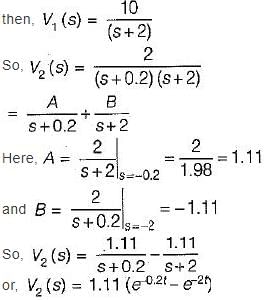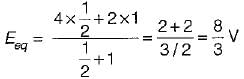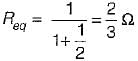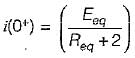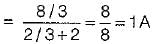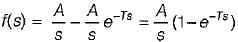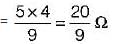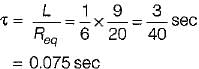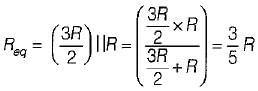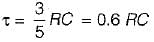Test: First Order RL & RC Circuits- 2 - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: First Order RL & RC Circuits- 2
The Laplace transform of the derivative of the signal f(t) = e-t u(t) is
For a series R - C circuit excited by a dc voltage of 20 V, and with time-constant τ seconds, the voltage across the capacitor at time t = τ is given by
The Laplace-transform equivalent of a given network will have 7/5 F capacitor replaced by 5
An RC circuit has a capacitor C = 2 μF in series with a resistance R = 1 MΩ The time of 6 secs will be equal to
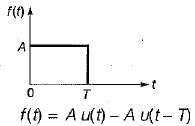
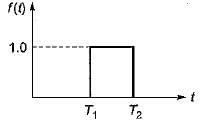
The Laplace transform of the gate function shown below is
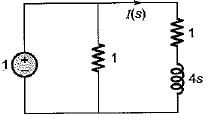
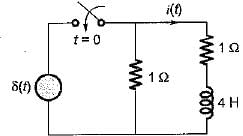
Assuming initial condition to be zero, the current i(t) in the circuit shown below is
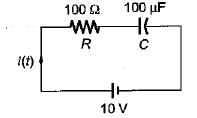
A 10 volts step voltage is applied across a RC series circuit at t = 0 having R = 100 Ω, and C = 100 μF.
The values of i(t) and di(t)/dt at t = 0 are respectively given by
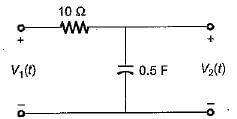
If the input voltage V1(t) = 10 e-2t V then, the output voltage V2(t) for the circuit shown below is
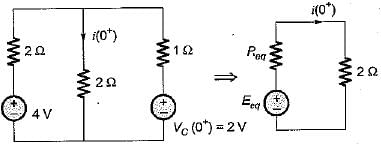
In the circuit shown below, the switch 'S' is opened at t = 0. Prior to that, switch was closed.
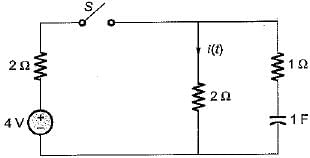
The current i(t) is at t = 0+ is
A rectangular pulse of duration T and magnitude A has the Laplace transform
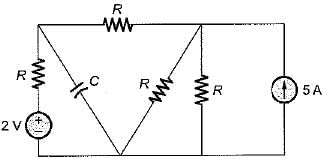
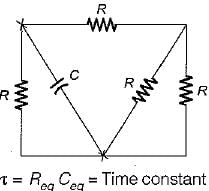
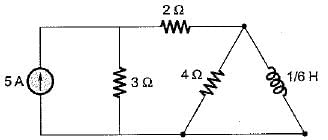
The time constant of the circuit shown below is
Assertion (A): Laplace transform is preferred for solving networks involving higher order differential equations.
Reason (R): The classical method for solving differential equations of higher order is quite cumbersome.
Assertion (A): In a purely capacitive circuit, the current wave is more distorted than the voltage wave.
Reason (R): The harmonics in the current wave are increased in proportion to their frequency numbers.
The time constant of the circuit shown below is