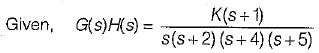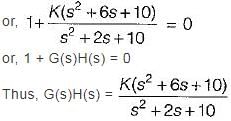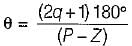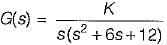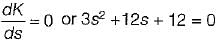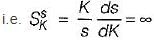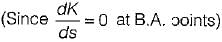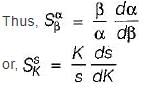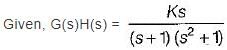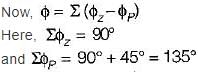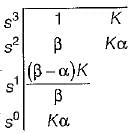Test: The Root Locus Technique- 2 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test GATE Electrical Engineering (EE) Mock Test Series 2026 - Test: The Root Locus Technique- 2
The open loop transfer function of a unity feedback control system is given by
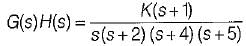
The breakaway point in its root locus will lie between
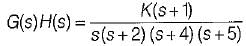
The breakaway point in its root locus will lie between
The characteristic equation of a closed loop control system is given by:
s2 + 2s +10 + K(s2 + 6s + 10) = 0
The angle of asymptotes for the root loci for K ≥ 0 are given by
s2 + 2s +10 + K(s2 + 6s + 10) = 0
The angle of asymptotes for the root loci for K ≥ 0 are given by
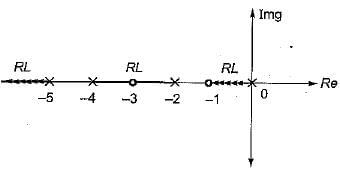
The breakaway point in the root loci plot for the loop transfer function
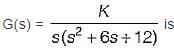
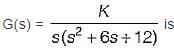
Consider the following statements pertaining to root locus techniques:
1. Routh-Hurwitz criterion may be used to find the intersections of the root loci on the imaginary axis.
2. Breakaway points on the root loci of an equation corresponds to multiple-order roots of the equation.
3. The breakaway points on the root loci of 1 + KG(s) H(s) = 0 must satisfy
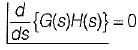
4. n root loci arrive or depart a breakaway point at 180/n degrees.
Which of these statements are correct?
Assertion (A): From the root sensitivity standpoint, a system should not be operated at the breakaway points.
Reason (R): The root sensitivity at the breakaway points is zero.
Consider the following statements:
1. All the rules and properties for the construction of root loci in the s-plane can be applied to the construction of root loci of discrete data system in the z-plane without any modification.
2. The breakaway points of the root loci must always be on the real axis.
3. There is only, one intersection of the asymptotes of the complex root loci.
4. Adding a pole to Q(s)/P(s) has the general effect of pushing the root loci to the left, whereas adding a zero pushes the loci to the right.
Which of the above statements is/are not correct related to root locus technique in control system?
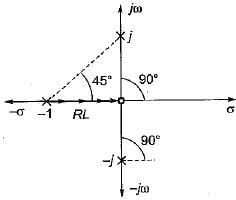
For the loop transfer function:

the angle of departure at s = j for K > 0 is
Which of the following is not true regarding the existence of breakaway point in root locus technique?
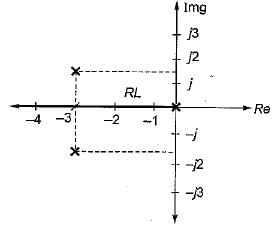
The open loop transfer function of a system is given by
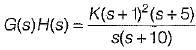
The number of loci terminating at infinity is
A unity feedback system has open-loop transfer function,
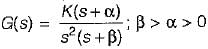
The valid root-loci for this system is
|
26 docs|257 tests
|
|
26 docs|257 tests
|