31 Year NEET Previous Year Questions: Oscillations - 1 - NEET MCQ
25 Questions MCQ Test - 31 Year NEET Previous Year Questions: Oscillations - 1
A particle of mass m oscillates with simple harmonic motion between points x1 and x2, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph. [2003]
The potential energy of a simple harmonic oscillator when the particle is half way to its end point is [2003]
where E is the total energy
In case of a forced vibration, the resonance wave becomes very sharp when the [2003]
The time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be
Which one of the following statements is true for the speed v and the acceleration a of a particle executing simple harmonic motion ?
Two spr ings of spring constants k1 and k2 are joined in series. The effective spring constant of the combin ation is given by [2004]
A particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4 cm/s. The frequency of its oscillation is
The potential energy of a long spring when stretched by 2cm is U. If the spring is stretched by 8 cm, the potential energy stored in it is
The phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is [2007]
The particle executing simple harmonic motion has a kinetic energy K0 cos2ωt . The maximum values of the potential energy and the total energy are respectively [2007]
A mass of 2.0 kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure. The mass of the spring and the pan is negligible. When pressed slightly and released the mass executes a simple harmonic motion. The spring constant is 200 N/m. What should be the minimum amplitude of the motion so that the mass gets detached from the pan (take g = 10 m/s2)?[2007]

A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is[2007]
Two simple harmonic motions of angular frequency 100 and 1000 rad s–1 have the same displacement amplitude. The ratio of their maximum accelerations is: [2008]
A point performs simple harmonic oscillation of period T and the equation of motion is given by x = a sin (ωt + π/6). After the elapse of what fraction of the time period the velocity of the point will be equal to half of its maximum velocity?
[2008]
A simple pendulum performs simple harmonic motion about x = 0 with an amplitude a and time period T. The speed of the pendulum at 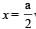 will be:[2009]
will be:[2009]
Which one of the following equations of motion represents simple harmonic motion? [2009]
where k, k0, k1 and a are all postive.
A block of mass M is attached to the lower end of a vertical spring. The spring is hung from a ceiling and has force constant value k. The mass is released from rest with the spring initially unstretched. The maximum extension produced in the length of the spring will be: [2009]
The displacement of a particle along the x-axis is given by x = a sin2ωt. The motion of the particle corresponds to: [2010]
The period of oscillation of a mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be [2010]
A par ticle of mass m is r eleased fr om rest and follows a parabolic path as shown.
Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time [2011]

Out of the following functions, representing motion of a particle, which represents SHM?
(A) y = sin ωt - cosωt [2011]
(B) y = sin3 ωt
(C) 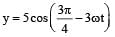
(D) y = 1 + ωt + ω2t2
Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is [2011M]
The damping force on an oscillator is directly proportional to the velocity. The units of the constant of proportionality are : [2012]
The equation of a simple harmonic wave is given by

Where x and y are in meters and t is in seconds.The ratio of maximum particle velocity to the wave velocity is [2012M]
A particle of mass m oscillates along x-axis according to equation x = a sinωt. The nature of the graph between momentum and displacement of the particle is [NEET Kar. 2013]


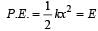
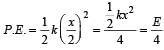

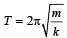

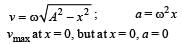

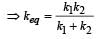
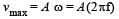


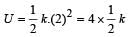
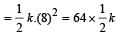
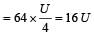
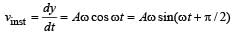
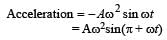
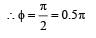
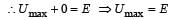
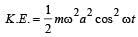
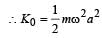
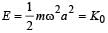
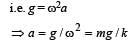
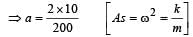
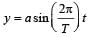
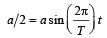
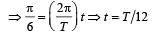
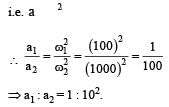
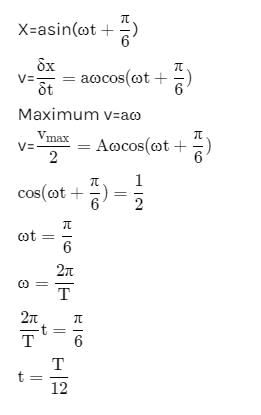
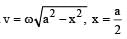
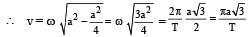
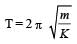


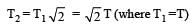


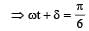
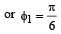

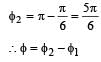
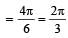
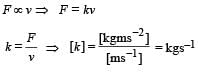
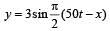
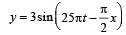 on comparing with the standard wave equation
on comparing with the standard wave equation
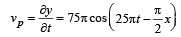
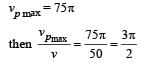
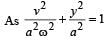 This is the equation ofellipse. Hence the graph is an ellipse. P versus x graph is similar to V versus x graph.
This is the equation ofellipse. Hence the graph is an ellipse. P versus x graph is similar to V versus x graph.










