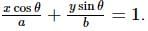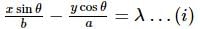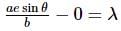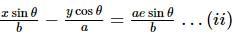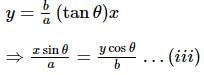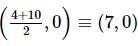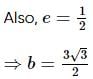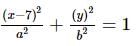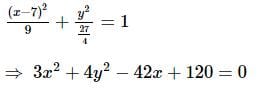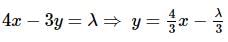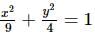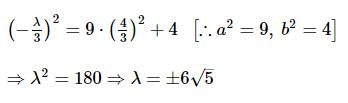BITSAT Mathematics Test - 10 - JEE MCQ
30 Questions MCQ Test - BITSAT Mathematics Test - 10
If α, β, γ are the roots of the equation 2x3 – 3x2 + 6x + 1 = 0, then α2 + β2 + γ2 is equal to:
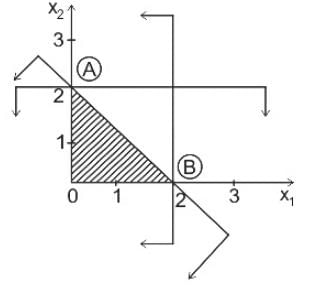
Consider the following Linear Programming Problem (LPP).
Maximise Z = x1 + 2x2
Subject to:
x1 ≤ 2
x2 ≤ 2
x1 + x2 ≤ 2
x1 + x2 ≥ 0 (i.e. +ve decision variables)
What is the optimal solution to the above LPP?
Maximise Z = x1 + 2x2
Subject to:
x1 ≤ 2
x2 ≤ 2
x1 + x2 ≤ 2
x1 + x2 ≥ 0 (i.e. +ve decision variables)
Find the median of this set of data : 34, 31, 37, 44, 38, 34, 43 & 41.
100 cards are numbered from 1 to 100. A card is picked up at random. Find the probability of getting a card with a perfect square number.
The condition that the straight line cx - by + b2 = 0 may touch the circle x2 + y2 = ax + by is: (a, b, c ≠ 0)
At what points on the curve x2 + y2 - 2x - 4y + 1 = 0, is the tangent parallel to the Y-axis?
If u = f(x3), v = g(x2), f′(x) = cos x and g′(x) = sin x = sin, then du/dv is
If y = (1 + x) (1 + x2) (1 + x4)…(1 + x2n), then dy/dx at x = 0 is:
If y = loge (sin(x2)), 0 < x < π/2, then dy/dx at x = √π/2 is
If 5f(x) + 3f(1/x) = x + 2 and y = x f(x), then (dy/dx)x = 1is equal to
The locus of the point which divides the double ordinates of the ellipse 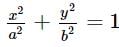 in the ratio 1 : 2 internally is :
in the ratio 1 : 2 internally is :
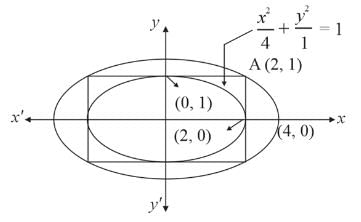
The ellipse x2 + 4y2 = 4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4,0). Then, the equation of the ellipse is
The eccentricity of a standard ellipse whose length of latus rectum is equal to distance between its foci is
The equation of normal at the point (0,3) of the ellipse 9x2 + 5y2 = 45, is
The focal distances of the point (4√3, 5) on the ellipse 25x2 + 16y2 = 1600 can be
If (√3)bx + ay = 2ab touches the ellipse 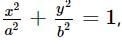 then eccentric angle of point of contact is
then eccentric angle of point of contact is
In an ellipse the locus of point of intersection of the perpendicular from a focus upon any tangent and the line joining the centre of the ellipse to the point of contact, is
The equation of an ellipse whose eccentricity is 1/2 and the vertices are (4, 0) and (10, 0)is
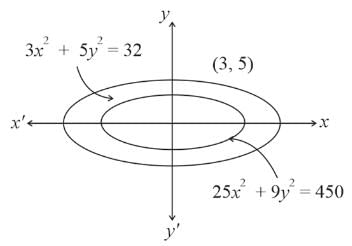
The total number of tangents through the points (3,5) that can be drawn to the ellipses 3x2 + 5y2 = 32 and 25x2 + 9y2 = 450 is
Equation of tangents to the ellipse 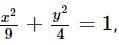 which are perpendicular to the line 3x + 4y = 7, are
which are perpendicular to the line 3x + 4y = 7, are


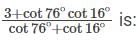



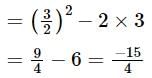

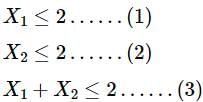
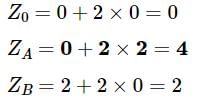
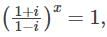 then which of the follwing is true?
then which of the follwing is true?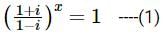
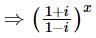
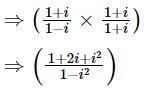

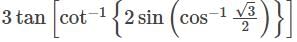

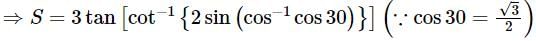
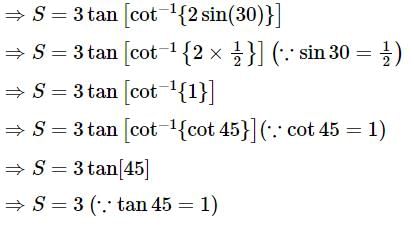
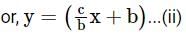
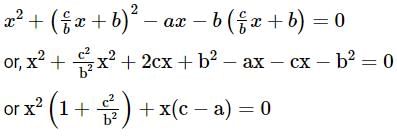
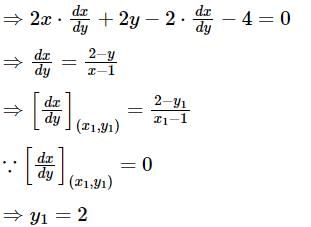
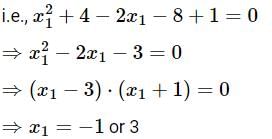
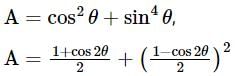

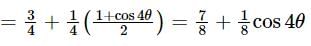
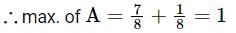
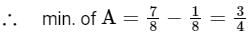
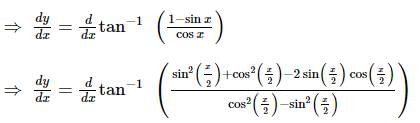
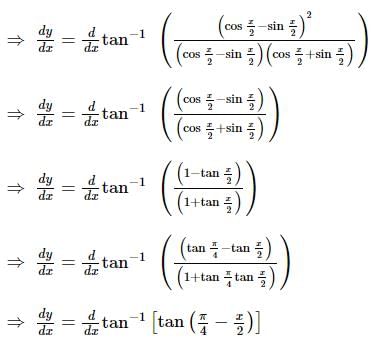
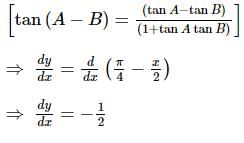

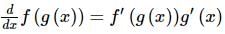
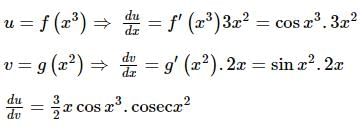
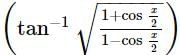 is equal to
is equal to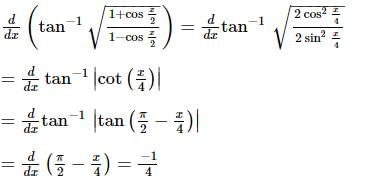

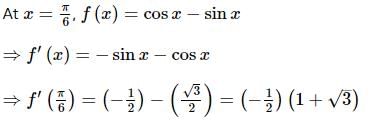
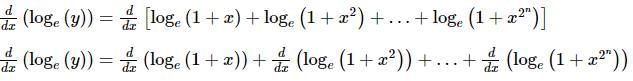
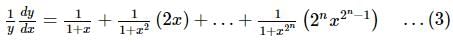
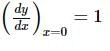

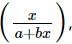 then
then  is equal to
is equal to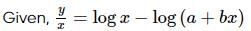
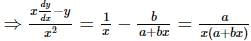 (differentiating both sides w.r.t. x)
(differentiating both sides w.r.t. x)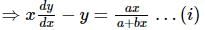
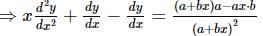 (again differentiating both sides w.r.t. x)
(again differentiating both sides w.r.t. x)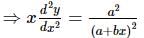
 (using the equation (i)).
(using the equation (i)).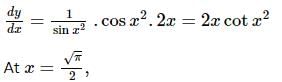
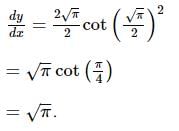
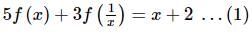
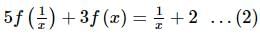
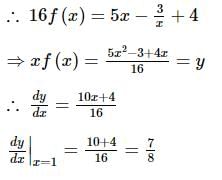

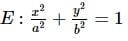
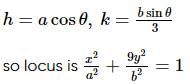
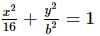
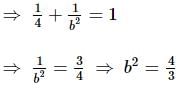
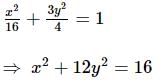
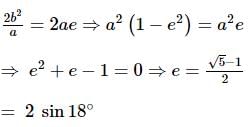
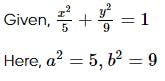
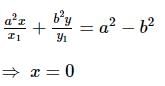
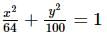
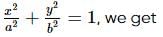

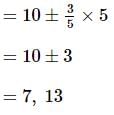
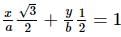 and equation of tangent at the point (a cos ϕ, b sin ϕ) on the ellipse is
and equation of tangent at the point (a cos ϕ, b sin ϕ) on the ellipse is 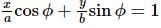
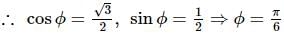
 can be taken as P(a cosθ, b sinθ)
can be taken as P(a cosθ, b sinθ)