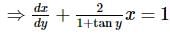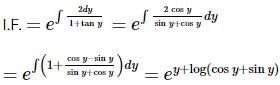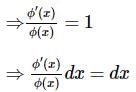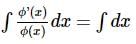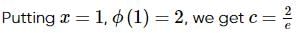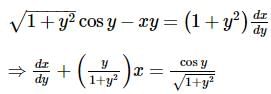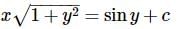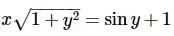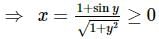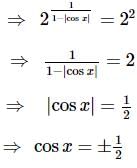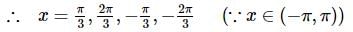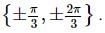BITSAT Mathematics Test - 6 - JEE MCQ
30 Questions MCQ Test - BITSAT Mathematics Test - 6
Consider the vector equation 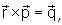
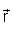 is a unit vector and
is a unit vector and 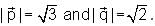
Which of the following statements is true?
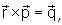
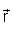 is a unit vector and
is a unit vector and 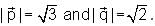
Which of the following statements is true?
A librarian puts a book in a bookshelf having 50 book slots which are now completely occupied. He puts the book at none of any extreme slots. When he visits the next working day, he finds that exactly 30 slots are still filled with the books. What is the probability that the slots on each side of his book are still vacant? (Assume each book belongs to different individuals)
Consider the equation of an ellipse:
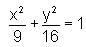
What is the distance (in units) of a chord AB from its centre, which is subtending 90o at the centre of the ellipse
Consider the matrix given below:
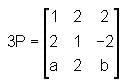
Also,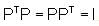 , where I is the identity matrix.
, where I is the identity matrix.
Mark the correct choice from the following options.
Consider the following function:
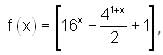 where [∙] denotes the greatest integer function.
where [∙] denotes the greatest integer function.
What is the range of the f(x)?
Consider the following function:
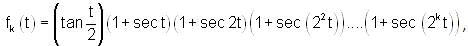 where k is a positive integer.
where k is a positive integer.
Which of the following statements are true?
i.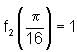
ii.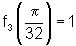
iii.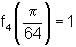
iv.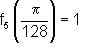
The differential equation obtained by eliminating arbitrary constants from y=aebx is
The solution of the differential equation 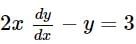 represents :
represents :
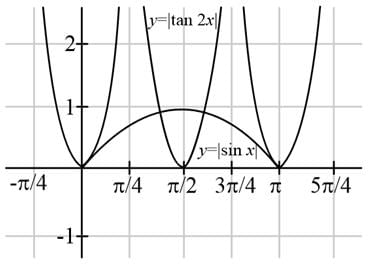
The number of solutions of equation |tan2x|=sinx in [0,π] is
Solution of the equation xdy−[y+xy3 (1 + log x)] dx = 0 is
he general solution of the differential equation (1 + tan y)(dx − dy) + 2x dy = 0 is
If the solution of the differential equation 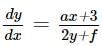 represents a circle, then the value of a is -
represents a circle, then the value of a is -
An integrating factor of the differential equation 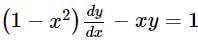 is
is
The equation of the curve passing through the point (1,1) such that the slope of the tangent at any point (x,y) is equal to the product of its co-ordinates is
The solution of the equation x(1+x2) dy = (y + y x2 – x2)dx is (c is constant of integration)
Which of the following is solution of the differential equation y′y′′′=3(y′′)2
The value of ( sin36° sin72° sin108° sin144°) is equal to
The greatest and least value of sin x cos are respectively
The general solution of the differential equation (1+tany)(dx−dy)+2xdy=0 is
Consider the differential equation 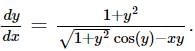 Also x=1 at y = 0 . Tick the appropriate option.
Also x=1 at y = 0 . Tick the appropriate option.
If x∈(−π, π) then find the number of solutions of the equation 21+|cosx|+∣∣cos2x∣∣+... = 4


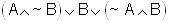 is the equivalent of
is the equivalent of
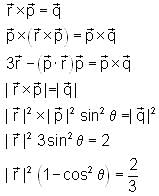
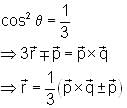


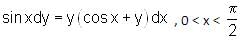
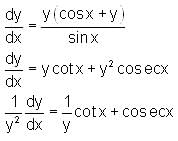
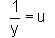
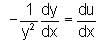
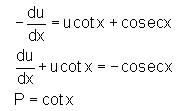

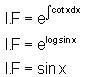
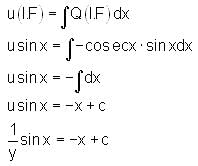
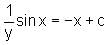
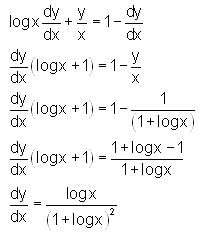
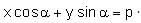

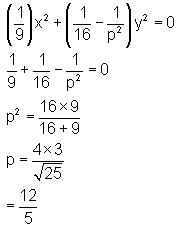
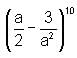 is
is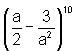 is:
is: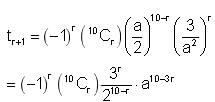
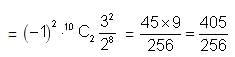
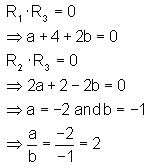
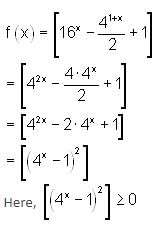
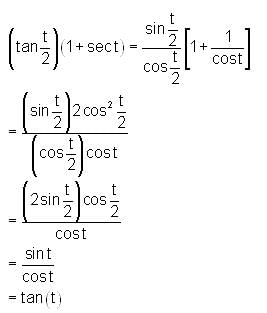

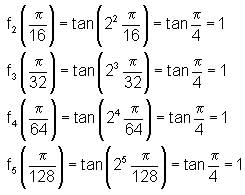
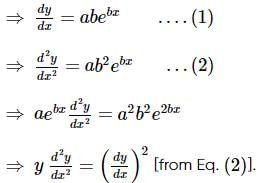
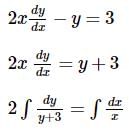
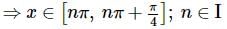




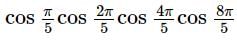 is equal to
is equal to
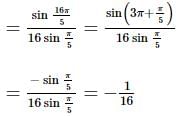
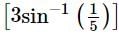 is equal to
is equal to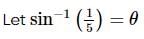
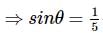
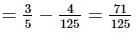
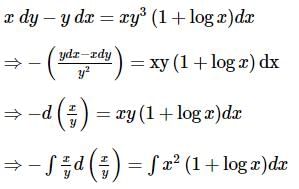
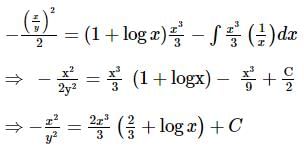
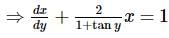
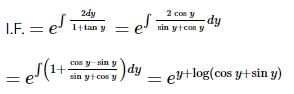
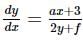

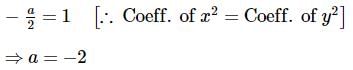
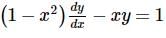
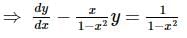
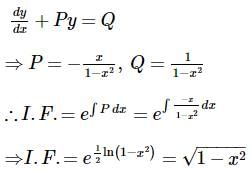
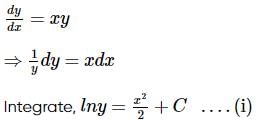
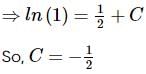
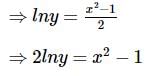
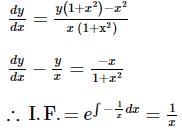
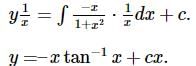
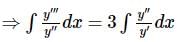
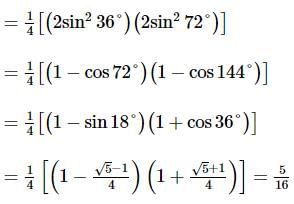
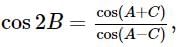 then tan A, tan B & tan C are in
then tan A, tan B & tan C are in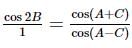
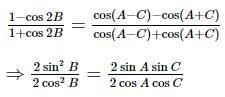
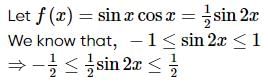
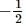 respectively.
respectively.