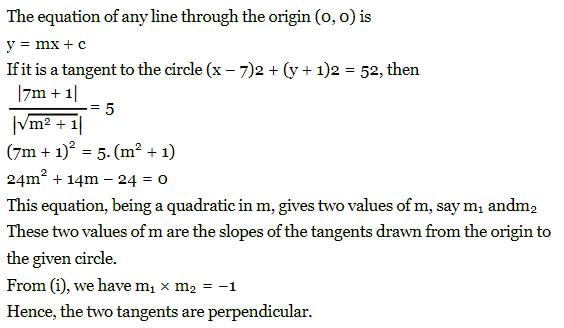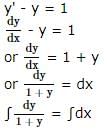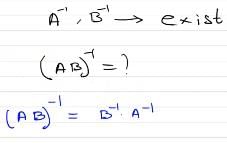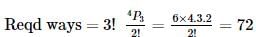BITSAT Maths Test - 5

The limiting point of the system of co-axial circles x²+y²-6x-6y+4=0, x²+y²-2x-4y+3=0 is

If [(1 + i√3)/(1 + i√3)]ⁿ is an integer ,then n is equal to

The differential equation for the family of curves x² + y² - 2ay = 0, where a is an arbitrary constant is

The number of points at which the function f(x)=|x-0.5|+|x-1|+tanx is not differentiable in (0,2) is

The solution of y'- y = 1, y(0) = 1 is given by y (x)

The general solution of the equation x²(dy/dx)=2 is

If y = sec tan^⁻1 x, then (dy/dx) =

Sum of the infinite series 1 + 3/2! + 6/3! + 10/4! + ...... is

If a flag staff of 6 mt high placed on the top of a tower throws a shadow of 2 √3 mt along the ground then the angle that the sun makes with the ground is

A variable straight line of slope 4 intersects the hyperbola xy = 1 at two points. The locus of the point which divides the line segment between these two points in the ratio 1:2 is

The general solution of the differential equation (dy/dx) = (x²/y²) is

The area bounded by the curve y² = 9x and the lines x = 1, x = 4 and y = 0 in the first quadrant is

Let f(x + y) = f(x)f(y) for all x and y. Suppose that f(3) = 3 and f′(0) = 11 then f′(3) is given by

A square matrix can always be expressed as a

If A and B are square matrices and A^⁻1 and B^⁻1 of same order exists, then (AB)^⁻1 is equal to

The curved surface of the cone inscribed in a given sphere is maximum if h=

If z is a complex number, then | 3z − 1 | = 3 | z − 2 | represents

The angle between lines given by x²+4y²-7xy=0 is

If x+y+1=0 tocuhes the parabola y²=λx,then λ is equal to

The line y=mx+c touches the parabola x²=4ay if

How many words are formed from the letters of the word EAMCET so that two vowels are never together?

Number of triangles formed by joining 12 points, no three of which are in the same straight line except 7 of them which are in a straight line, is

The mean and variance of a Binomial distribution are 6 and 4. The parameter n is

Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is

In 

In Δ A B C , i f a = 2, b = 3, c = 4, then cos A =

If the sum of the roots of the quadratic equation ax²+bx+c = 0, is equal to the sum of the squares of their reciprocals, then (a/c), (b/a), (c/b) are in

The value of 0.234 is

If a, b, c, d, e, f are in A.P. then e - c is equal to

If f (x) = (1)/(1 - x), then f[f{f (x)}] =

2 [tan^⁻1(1/2) + tan^⁻1(1/3) + tan^⁻11] is equal to

The coordinates of mid-point of portion of line cut by coordinate axis are (3,2), the equation of the line is

A tetrahedron has vertices at O (0, 0, 0), A(1, 2, 1), B(2, 1, 3) and C (-1, 1, 2). Then the angle between the faces OAB and ABC will be

The angle between the curves y² = x, x² = y at (1,1) is

The direction ratios of the diagonals of a cube which joins the origin to the opposite corner are (when the 3 concurrent edges of the cube are co-ordinate axes)

In any right angled triangle hypotenuse is equal to 2√2 times the perpendicular drawn from the opposite vertex on it, then other angles are

If 2sec2α = tanβ + cotβ, then one of the value of (α+β) is

If sin 2x=n sin 2y, then the value of tan (x+y)/tan(x-y) is

The moment of force F=i+2j+3k about the point 2i-j+k is

The moment of the couple formed by the forces a n d acting at the points (9,−1,2) and (3,−2,1) respectively is