All Courses
Get the App Signup / Login
Sign in Open App
CAT Exam  >  CAT Tests  >  CAT DI And LR Mock Test - 2 - CAT MCQ

CAT DI And LR Mock Test - 2 - CAT MCQ


Test Description

25 Questions MCQ Test - CAT DI And LR Mock Test - 2

CAT DI And LR Mock Test - 2 for CAT 2024 is part of CAT preparation. The CAT DI And LR Mock Test - 2 questions and answers have been prepared according to the CAT exam syllabus.The CAT DI And LR Mock Test - 2 MCQs are made for CAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for CAT DI And LR Mock Test - 2 below.
Solutions of CAT DI And LR Mock Test - 2 questions in English are available as part of our course for CAT & CAT DI And LR Mock Test - 2 solutions in Hindi for CAT course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt CAT DI And LR Mock Test - 2 | 25 questions in 35 minutes | Mock test for CAT preparation | Free important questions MCQ to study for CAT Exam | Download free PDF with solutions
CAT DI And LR Mock Test - 2 - Question 1
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

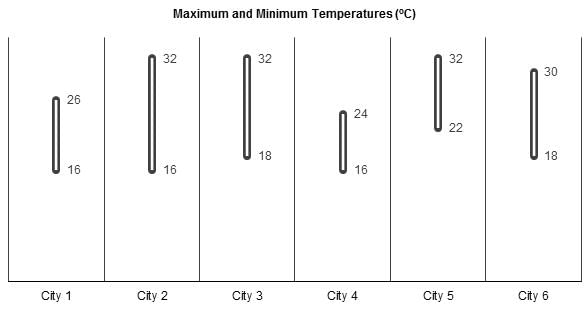
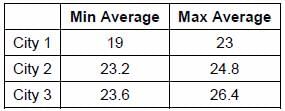
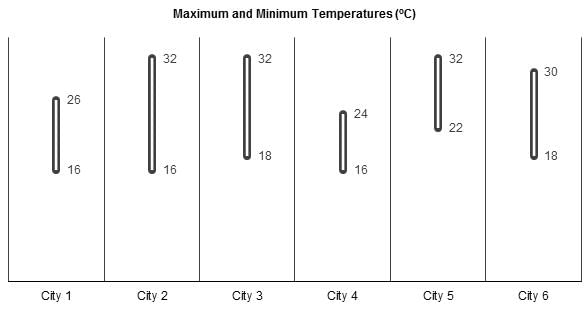
A meteorological agency measured the temperatures (in oC) across six cities for ten consecutive days. Every day, the agency measured the temperature in each city exactly once and at a specified time of the day. The agency also observed that, during this ten-day period, the temperature in any city across two consecutive days either remained constant or changed by exactly 2oC. The following chart provides the maximum and the minimum temperature recorded during the ten days for each city.

Q. If it is known that the average temperature over the ten days in one of the six cities was 25oC, which of the following cities can it be?

Detailed Solution for CAT DI And LR Mock Test - 2 - Question 1
For each city, the average will be the minimum possible if the minimum temperature is present for the maximum number of days, and the average will be the maximum possible if the maximum temperature is present for the maximum number of days. For City 1, the minimum average will be the average of 16, 16, 16, 16, 16, 18, 20, 22, 24, 26 i.e., 19°C. The maximum average will be the average of 16, 18, 20, 22, 24, 26, 26, 26, 26, 26 i.e., 23°C.

Similarly calculating the maximum and minimum average for the remaining cities,

Hence, only City 3 can have an average temperature of 25°C.

CAT DI And LR Mock Test - 2 - Question 2
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

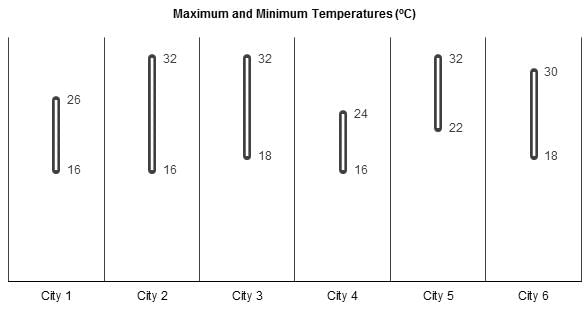
A meteorological agency measured the temperatures (in oC) across six cities for ten consecutive days. Every day, the agency measured the temperature in each city exactly once and at a specified time of the day. The agency also observed that, during this ten-day period, the temperature in any city across two consecutive days either remained constant or changed by exactly 2oC. The following chart provides the maximum and the minimum temperature recorded during the ten days for each city.

Q. If any day on which all the six cities had the same temperature is called an ‘isothermal’ day, then what is the maximum possible number of ‘isothermal’ days during the given period?

Detailed Solution for CAT DI And LR Mock Test - 2 - Question 2
If all the cities are to have the same temperature, the temperature has to be either 22°C or 24°C because the maximum temperature of City 4 is 24°C and the minimum temperature of City 5 is 22°C. The maximum number of days that all the cities can have the same temperatures (22°C or 24°C) is determined by City 2 because the temperature of this city show the highest variation. In City 2, the temperature could have been 22°C or 24°C for a maximum of 3 days (2 days at 22°C and 1 day at 24°C or vice versa) as it will take 9 days for the temperature to reach from one extreme to the other. In all the other cities, the temperature can be 22°C or 24°C for more than 2 days. Therefore, across all the cities, the temperature can be 22°C for 2 days and 24°C for 1 day or vice versa.

In either case, the maximum number of days for which the temperature can be the same across all the cities is 3.

1 Crore+ students have signed up on EduRev. Have you? Download the App
CAT DI And LR Mock Test - 2 - Question 3
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

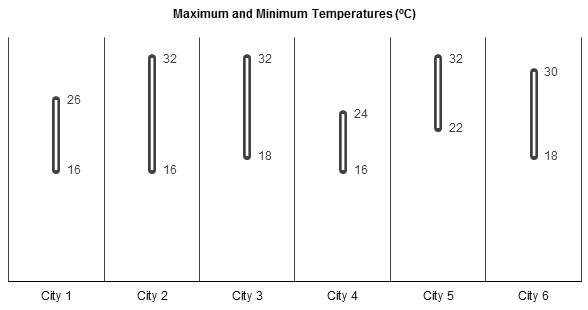
A meteorological agency measured the temperatures (in oC) across six cities for ten consecutive days. Every day, the agency measured the temperature in each city exactly once and at a specified time of the day. The agency also observed that, during this ten-day period, the temperature in any city across two consecutive days either remained constant or changed by exactly 2oC. The following chart provides the maximum and the minimum temperature recorded during the ten days for each city.

Q. On which of the following days can all the six cities have a temperature of 22oC?

Detailed Solution for CAT DI And LR Mock Test - 2 - Question 3
For City 2, the initial temperature can only be 16 or 18 or 30 or 32. In any other case, the minimum and the maximum temperatures for the city cannot be possible. In these cases, only days 4, 5, 6, and 7 can have a temperature of 22°C. From the given options, only Day 7 can have a temperature of 22°C.

CAT DI And LR Mock Test - 2 - Question 4
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

A meteorological agency measured the temperatures (in oC) across six cities for ten consecutive days. Every day, the agency measured the temperature in each city exactly once and at a specified time of the day. The agency also observed that, during this ten-day period, the temperature in any city across two consecutive days either remained constant or changed by exactly 2oC. The following chart provides the maximum and the minimum temperature recorded during the ten days for each city.

Q. If the temperature of City 3 is 26oC on day 5, which of the following can be the average temperature for this city over the ten days?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 4
For City 3, the minimum temperature has to be 18°C and the maximum temperature has to be 32°C. The average temperature across the 10 days will be the minimum if the total temperature across the 10 days is least and vice versa. The following cases show the minimum and maximum possible averages

From the options, only option B and option C fall within this range. However, the value given in option C cannot be the average temperature across ten days because then the sum of the temperatures across the ten days has to be 263. Since the sum of ten even numbers cannot be odd, this is not possible. Hence, option B is the right answer.

CAT DI And LR Mock Test - 2 - Question 5
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

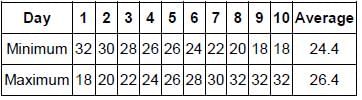
A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:

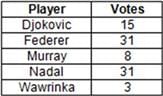
Further, it is also known that,

i. Murray was the only player who received the same number of votes in two or more rounds.

ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.

iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.

iv. in none of the rounds did more than one player receive the least number of votes.

Q. How many votes did Federer receive in the third round?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 5
From the table we can see that Wawrinka must have been eliminated in the first round because he received only three votes. None of the other players could have received less than three votes, Hence, Wawrinka received three votes in the first round, In the second round, these 3 votes must be distributed across the remaining players. From (iii), Murray must have received at least 4 votes in the first round. Hence, he must have received 4 votes in the first and second rounds (from (i)). (Since he could not have received the same number of votes in at least two rounds - two votes each In rounds 2 and 3 is not possible because of (ii)). Since Murray is the only player to receive the same number of votes across at least two rounds, the remaining players must have had an increase in the number of votes that they received. Therefore, Djokovic, Federer and Nadal must each have received one additional vote in round 2. Djokovic must have received at least 4 votes in Round 1. Hence, he must have received at least 5 votes in Round 2. Also, Federer and Nadal could not have been eliminated in the 2nd round. Hence, Murray must have been eliminated in the second round. His 4 votes must be distributed across the remaining three players. Let a be the number of votes that Djokovic received in the first round, Hence, he must have received a+1 votes in the second round. In the third round, he must have received a+2 or a+3 votes (since the number of votes of Federer and Nadal must also have Increased by one each). Since Djokovic received a total of 15 voles, either 3a+3 or 3a+4, For a to be an integer, only 3a+3 is possible and a = 4, Hence, Djokovic received 4, 5, 6 votes in 1st, 2nd and 3rd rounds respectively. Let b and c denote the number of votes that Federer and Nadal received during the first round. In the second round, they must have received b+1 and c+1. Since b+c =11 (as there are 22 members i.e., 22 votes), b and c can only be 5 and 6 In any order, (b and c cannot be 4 since only two players received the same number of votes and b and c cannot be 3 from (iii)). In the second round, they must have received 6 and 7 votes. Since they could not have received the same number of votes in the final round (from (iv)), they must have received the same number of votes in round 3. Hence, they must have got 8 votes each in the third round. In the final round, they must have got 12 and 10 votes for them to have a total of 31 votes,

The following table gives the votes received by each player in each round.

Federer received 8 votes in Round 3,

CAT DI And LR Mock Test - 2 - Question 6
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:

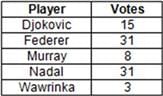
Further, it is also known that,

i. Murray was the only player who received the same number of votes in two or more rounds.

ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.

iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.

iv. in none of the rounds did more than one player receive the least number of votes.

Q. In which of the following rounds did at least two players receive the same number of votes?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 6
From the table we can see that Wawrinka must have been eliminated in the first round because he received only three votes. None of the other players could have received less than three votes, Hence, Wawrinka received three votes in the first round, In the second round, these 3 votes must be distributed across the remaining players. From (iii), Murray must have received at least 4 votes in the first round. Hence, he must have received 4 votes in the first and second rounds (from (i)). (Since he could not have received the same number of votes in at least two rounds - two votes each In rounds 2 and 3 is not possible because of (ii)). Since Murray is the only player to receive the same number of votes across at least two rounds, the remaining players must have had an increase in the number of votes that they received. Therefore, Djokovic, Federer and Nadal must each have received one additional vote in round 2. Djokovic must have received at least 4 votes in Round 1. Hence, he must have received at least 5 votes in Round 2. Also, Federer and Nadal could not have been eliminated in the 2nd round. Hence, Murray must have been eliminated in the second round. His 4 votes must be distributed across the remaining three players. Let a be the number of votes that Djokovic received in the first round, Hence, he must have received a+1 votes in the second round. In the third round, he must have received a+2 or a+3 votes (since the number of votes of Federer and Nadal must also have Increased by one each). Since Djokovic received a total of 15 voles, either 3a+3 or 3a+4, For a to be an integer, only 3a+3 is possible and a = 4, Hence, Djokovic received 4, 5, 6 votes in 1st, 2nd and 3rd rounds respectively. Let b and c denote the number of votes that Federer and Nadal received during the first round. In the second round, they must have received b+1 and c+1. Since b+c =11 (as there are 22 members i.e., 22 votes), b and c can only be 5 and 6 In any order, (b and c cannot be 4 since only two players received the same number of votes and b and c cannot be 3 from (iii)). In the second round, they must have received 6 and 7 votes. Since they could not have received the same number of votes in the final round (from (iv)), they must have received the same number of votes in round 3. Hence, they must have got 8 votes each in the third round. In the final round, they must have got 12 and 10 votes for them to have a total of 31 votes,

The following table gives the votes received by each player in each round.

In Round 3, two players received the same number of votes.

CAT DI And LR Mock Test - 2 - Question 7
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:

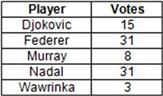
Further, it is also known that,

i. Murray was the only player who received the same number of votes in two or more rounds.

ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.

iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.

iv. in none of the rounds did more than one player receive the least number of votes.

Q. If Federer received more votes than exactly three other players in the first round, which player was declared the best tennis player in the world?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 7
From the table we can see that Wawrinka must have been eliminated in the first round because he received only three votes. None of the other players could have received less than three votes, Hence, Wawrinka received three votes in the first round, In the second round, these 3 votes must be distributed across the remaining players. From (iii), Murray must have received at least 4 votes in the first round. Hence, he must have received 4 votes in the first and second rounds (from (i)). (Since he could not have received the same number of votes in at least two rounds - two votes each In rounds 2 and 3 is not possible because of (ii)). Since Murray is the only player to receive the same number of votes across at least two rounds, the remaining players must have had an increase in the number of votes that they received. Therefore, Djokovic, Federer and Nadal must each have received one additional vote in round 2. Djokovic must have received at least 4 votes in Round 1. Hence, he must have received at least 5 votes in Round 2. Also, Federer and Nadal could not have been eliminated in the 2nd round. Hence, Murray must have been eliminated in the second round. His 4 votes must be distributed across the remaining three players. Let a be the number of votes that Djokovic received in the first round, Hence, he must have received a+1 votes in the second round. In the third round, he must have received a+2 or a+3 votes (since the number of votes of Federer and Nadal must also have Increased by one each). Since Djokovic received a total of 15 voles, either 3a+3 or 3a+4, For a to be an integer, only 3a+3 is possible and a = 4, Hence, Djokovic received 4, 5, 6 votes in 1st, 2nd and 3rd rounds respectively. Let b and c denote the number of votes that Federer and Nadal received during the first round. In the second round, they must have received b+1 and c+1. Since b+c =11 (as there are 22 members i.e., 22 votes), b and c can only be 5 and 6 In any order, (b and c cannot be 4 since only two players received the same number of votes and b and c cannot be 3 from (iii)). In the second round, they must have received 6 and 7 votes. Since they could not have received the same number of votes in the final round (from (iv)), they must have received the same number of votes in round 3. Hence, they must have got 8 votes each in the third round. In the final round, they must have got 12 and 10 votes for them to have a total of 31 votes,

The following table gives the votes received by each player in each round.

If Federer received more votes than exactly 3 other players in the first round, Federer would have received 5 votes in the first round and 12 in the final round- Hence. Federer was declared the best tennis player in the world.

CAT DI And LR Mock Test - 2 - Question 8
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

A twenty-two-member panel was constituted to select the best tennis player in the world from five players - Federer, Nadal, Djokovic, Murray and Wawrinka. This selection was done in four rounds, such that in each round, the player that received the minimum number of votes was eliminated. The player that received the maximum number of votes in the final round was declared the best tennis player in the world. All the twenty-two members voted in all the four rounds and in each round, one member can vote for exactly one player. The following table gives the total number of votes received by each player across all the rounds:

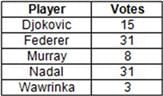
Further, it is also known that,

i. Murray was the only player who received the same number of votes in two or more rounds.

ii. all the members who voted for a specific player in a round voted for the same player in all the subsequent rounds unless he was eliminated.

iii. there were exactly two rounds in which the number of votes received by all the players were distinct, and exactly two rounds in which exactly two players received the same number of votes, while the others received a distinct number of votes each.

iv. in none of the rounds did more than one player receive the least number of votes.

Q. What is the total number of members in the panel who had to change the player that they voted for during any of the four rounds of voting?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 8
From the table we can see that Wawrinka must have been eliminated in the first round because he received only three votes. None of the other players could have received less than three votes, Hence, Wawrinka received three votes in the first round, In the second round, these 3 votes must be distributed across the remaining players. From (iii), Murray must have received at least 4 votes in the first round. Hence, he must have received 4 votes in the first and second rounds (from (i)). (Since he could not have received the same number of votes in at least two rounds - two votes each In rounds 2 and 3 is not possible because of (ii)). Since Murray is the only player to receive the same number of votes across at least two rounds, the remaining players must have had an increase in the number of votes that they received. Therefore, Djokovic, Federer and Nadal must each have received one additional vote in round 2. Djokovic must have received at least 4 votes in Round 1. Hence, he must have received at least 5 votes in Round 2. Also, Federer and Nadal could not have been eliminated in the 2nd round. Hence, Murray must have been eliminated in the second round. His 4 votes must be distributed across the remaining three players. Let a be the number of votes that Djokovic received in the first round, Hence, he must have received a+1 votes in the second round. In the third round, he must have received a + 2 or a + 3 votes (since the number of votes of Federer and Nadal must also have Increased by one each). Since Djokovic received a total of 15 voles, either 3a + 3 or 3a + 4, For a to be an integer, only 3a + 3 is possible and a = 4, Hence, Djokovic received 4, 5, 6 votes in 1st, 2nd and 3rd rounds respectively. Let b and c denote the number of votes that Federer and Nadal received during the first round. In the second round, they must have received b + 1 and c + 1. Since b + c = 11 (as there are 22 members i.e., 22 votes), b and c can only be 5 and 6 In any order, (b and c cannot be 4 since only two players received the same number of votes and b and c cannot be 3 from (iii)). In the second round, they must have received 6 and 7 votes. Since they could not have received the same number of votes in the final round (from (iv)), they must have received the same number of votes in round 3. Hence, they must have got 8 votes each in the third round. In the final round, they must have got 12 and 10 votes for them to have a total of 31 votes,

The following table gives the votes received by each player in each round.

Except for the members who voted for Federer and Nadal in the first round, the remaining members had to change the player that they voted for i.e., 11 members changed the player that they voted for.

CAT DI And LR Mock Test - 2 - Question 9
Save

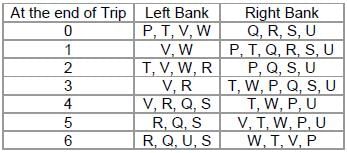
Four persons, Pavan, Tarun, Venky, and Waqar, are standing on the left bank of a river, whereas another four persons, Qureshi, Ramesh, Sanjay, and Uday, are standing on the right bank of the river. A ferry, which can be used to cross the river and go to the other bank, is present initially on the left bank. The ferry can carry a maximum of two people at a time. However, there must be at least one person in the ferry in order to guide it to the other bank. The travel of the ferry from one bank to the other is called a trip. The eight persons have certain preferences regarding how they would like to travel in the ferry. The following information is known about their preferences:

i. If Pavan is present in the ferry, Tarun must also be present in the ferry.

ii. If Venky travels to a bank on which Sanjay is already present, Sanjay will immediately travel to the opposite bank.

iii. Qureshi will travel in the ferry only when Uday is not present in the ferry.

iv. Venky and Waqar cannot travel together in the ferry.

Q. What is the minimum number of trips the ferry must make so that all the eight people are present on the same bank?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 9

Let P, Q, R, S, T, U, V, and W represent the eight people.

If all the eight people are to be present on the left bank, it would require at least eight trips. This is because, since the ferry is on the left bank, it will take two trips to bring one person from the right bank to the left bank (one person from left bank will go to the right bank and return with another person from the right bank). If they were to converge on the right bank, the minimum number of trips it would take is 5. T and P from the left bank can go to the right bank first. S has to return with the ferry and take one more person, V, to the right bank. S will travel back and return with W. This will repeat until everyone moves to the right bank. Hence the answer is 5.

CAT DI And LR Mock Test - 2 - Question 10
Save

Four persons, Pavan, Tarun, Venky, and Waqar, are standing on the left bank of a river, whereas another four persons, Qureshi, Ramesh, Sanjay, and Uday, are standing on the right bank of the river. A ferry, which can be used to cross the river and go to the other bank, is present initially on the left bank. The ferry can carry a maximum of two people at a time. However, there must be at least one person in the ferry in order to guide it to the other bank. The travel of the ferry from one bank to the other is called a trip. The eight persons have certain preferences regarding how they would like to travel in the ferry. The following information is known about their preferences:

i. If Pavan is present in the ferry, Tarun must also be present in the ferry.

ii. If Venky travels to a bank on which Sanjay is already present, Sanjay will immediately travel to the opposite bank.

iii. Qureshi will travel in the ferry only when Uday is not present in the ferry.

iv. Venky and Waqar cannot travel together in the ferry.

Q. If Tarun and Ramesh are in the ferry during its second trip, what is the minimum number of trips in which all the people on the left bank could go to the right bank and vice versa?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 10
Let P, Q, R, S, T, U, V, and W represent the eight people.

If Tarun is present in the ferry in the second trip, he must have been in the ferry in the first trip as well. Since Tarun has to travel twice between the two banks in this case, the number of trips has to be at least six (more than the minimum number of trips obtained above). The following table shows one possible way in which this can be done in six trips.

Hence, this can be done in a minimum of six trips.

CAT DI And LR Mock Test - 2 - Question 11
Save

Four persons, Pavan, Tarun, Venky, and Waqar, are standing on the left bank of a river, whereas another four persons, Qureshi, Ramesh, Sanjay, and Uday, are standing on the right bank of the river. A ferry, which can be used to cross the river and go to the other bank, is present initially on the left bank. The ferry can carry a maximum of two people at a time. However, there must be at least one person in the ferry in order to guide it to the other bank. The travel of the ferry from one bank to the other is called a trip. The eight persons have certain preferences regarding how they would like to travel in the ferry. The following information is known about their preferences:

i. If Pavan is present in the ferry, Tarun must also be present in the ferry.

ii. If Venky travels to a bank on which Sanjay is already present, Sanjay will immediately travel to the opposite bank.

iii. Qureshi will travel in the ferry only when Uday is not present in the ferry.

iv. Venky and Waqar cannot travel together in the ferry.

Q. If Ramesh and Uday are in the ferry during its second trip, who among the following could not have travelled in the ferry during its first trip?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 11
If Venky had travelled in the first trip, Sanjay must be in the ferry in its second trip. Hence, Venky could not have travelled in the first trip.

CAT DI And LR Mock Test - 2 - Question 12
Save

Four persons, Pavan, Tarun, Venky, and Waqar, are standing on the left bank of a river, whereas another four persons, Qureshi, Ramesh, Sanjay, and Uday, are standing on the right bank of the river. A ferry, which can be used to cross the river and go to the other bank, is present initially on the left bank. The ferry can carry a maximum of two people at a time. However, there must be at least one person in the ferry in order to guide it to the other bank. The travel of the ferry from one bank to the other is called a trip. The eight persons have certain preferences regarding how they would like to travel in the ferry. The following information is known about their preferences:

i. If Pavan is present in the ferry, Tarun must also be present in the ferry.

ii. If Venky travels to a bank on which Sanjay is already present, Sanjay will immediately travel to the opposite bank.

iii. Qureshi will travel in the ferry only when Uday is not present in the ferry.

iv. Venky and Waqar cannot travel together in the ferry.

Q. After the ferry completed three trips, which of the following pairs of persons cannot be on the left bank?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 12
Qureshi and Uday could not have travelled together in the ferry. Hence, for them to come from right bank to left bank, the ferry would have to make at least two trips from right bank to left bank. Since this is not the case, Qureshi and Uday could not have been on the left bank.

CAT DI And LR Mock Test - 2 - Question 13
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

The capital city of the kingdom of Alami has the royal palace in the centre, with five fortifications, labelled F1 to F5, surrounding the palace. All the Alami soldiers are always present at the royal palace unless ordered to move to a fortification. An enemy kingdom Bagami planned to attack the royal palace and built camps around the fortifications. The Bagamis built seven camps - E1 to E7 - around the Alami fortifications and each Bagami camp had a certain number of soldiers. The soldiers from a given Bagami camp can attack only some of the fortifications, as indicated in the diagram below. However, all the soldiers from a single Bagami camp need not necessarily attack the same fortification. The Alami king came to know about this and was planning to send his soldiers to the fortifications.

The following diagram shows the royal palace (P), fortifications (F1 to F5) and enemy (Bagami) camps (E1 to E7). The solid lines in the figure represent the respective fortification to which the Alami soldiers can be deployed from the palace. The dotted lines from each enemy camp represent the fortifications that the soldiers from that enemy camp can attack. The numbers inside each enemy camp represent the number of soldiers stationed in that camp.

Assume that all the Bagami soldiers attack the fortifications that they are assigned to at the same time and each soldier will attack exactly one fortification. Also, a higher numerical strength in terms of soldiers will assure victory to any side in such a manner that, if, say, 10 Bagami soldiers attack a fortification with 11 Alami soldiers, all the Bagami soldiers will die and the fortification will remain safe, but with only 1 Alami soldier remaining alive. If the number of Bagami soldiers attacking a fortification is equal to the number of Alami soldiers at the fortification, all the soldiers belonging to both the sides will die but the fortification will remain safe. In a similar manner, if the number of Bagami soldiers attacking is in excess of the number of Alami soldiers, the fortification will be destroyed, but with only the excess number of Bagami soldiers remaining alive.

Q. What is the minimum number of soldiers the Alami king must deploy to all the fortifications put together in order to ensure that none of the fortifications is destroyed?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 13
If none of the fortifications must be destroyed, each fortification must have enough soldiers to fight against all the enemy camps that can attack that fortification.

Number of soldiers in F1 =38+ 69 + 42 + 51 = 200

Number of soldiers in F2 = 69 + 42 + 51 + 33 = 195

Number of soldiers in F3 = 51 + 33 + 48 = 132

Number of soldiers in F4 = 33 + 48 + 28 = 109

Number of soldiers in F5 = 69 + 28 + 38 = 135

Total number of soldiers across all fortifications = 200 + 195 + 132 + 109 + 135 = 771

CAT DI And LR Mock Test - 2 - Question 14
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

The capital city of the kingdom of Alami has the royal palace in the centre, with five fortifications, labelled F1 to F5, surrounding the palace. All the Alami soldiers are always present at the royal palace unless ordered to move to a fortification. An enemy kingdom Bagami planned to attack the royal palace and built camps around the fortifications. The Bagamis built seven camps - E1 to E7 - around the Alami fortifications and each Bagami camp had a certain number of soldiers. The soldiers from a given Bagami camp can attack only some of the fortifications, as indicated in the diagrambelow. However, all the soldiers from a single Bagami camp need not necessarily attack the same fortification. The Alami king came to know about this and was planning to send his soldiers to the fortifications.

The following diagram shows the royal palace (P), fortifications (F1 to F5) and enemy (Bagami) camps (E1 to E7). The solid lines in the figure represent the respective fortification to which the Alami soldiers can be deployed from the palace. The dotted lines from each enemy camp represent the fortifications that the soldiers from that enemy camp can attack. The numbers inside each enemy camp represent the number of soldiers stationed in that camp.

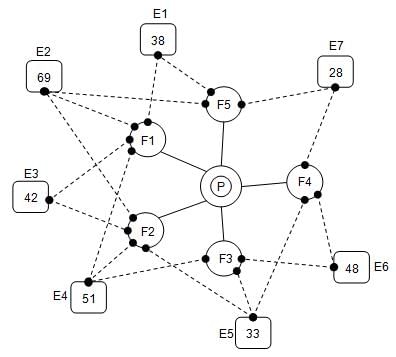
Assume that all the Bagami soldiers attack the fortifications that they are assigned to at the same time and each soldier will attack exactly one fortification. Also, a higher numerical strength in terms of soldiers will assure victory to any side in such a manner that, if, say, 10 Bagami soldiers attack a fortification with 11 Alami soldiers, all the Bagami soldiers will die and the fortification will remain safe, but with only 1 Alami soldier remaining alive. If the number of Bagami soldiers attacking a fortification is equal to the number of Alami soldiers at the fortification, all the soldiers belonging to both the sides will die but the fortification will remain safe. In a similar manner, if the number of Bagami soldiers attacking is in excess of the number of Alami soldiers, the fortification will be destroyed, but with only the excess number of Bagami soldiers remaining alive.

Q. If the Alami king wants to save at least three fortifications from being destroyed, what is the minimum number of soldiers that he must deploy?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 14
If three fortifications are to be saved from destruction, minimum of soldiers will be required to protect F3, F4 and F5. Hence, total number of soldiers required = 132+ 109+ 135 = 376.

CAT DI And LR Mock Test - 2 - Question 15
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

The capital city of the kingdom of Alami has the royal palace in the centre, with five fortifications, labelled F1 to F5, surrounding the palace. All the Alami soldiers are always present at the royal palace unless ordered to move to a fortification. An enemy kingdom Bagami planned to attack the royal palace and built camps around the fortifications. The Bagamis built seven camps - E1 to E7 - around the Alami fortifications and each Bagamicamp had a certain number of soldiers. The soldiers from a given Bagami camp can attack only some of the fortifications, as indicated in the diagrambelow. However, all the soldiers from a single Bagami camp need not necessarily attack the same fortification. The Alami king came to know about this and was planning to send his soldiers to the fortifications.

The following diagram shows the royal palace (P), fortifications (F1 to F5) and enemy (Bagami) camps (E1 to E7). The solid lines in the figure represent the respective fortification to which the Alami soldiers can be deployed from the palace. The dotted lines from each enemy camp represent the fortifications that the soldiers from that enemy camp can attack. The numbers inside each enemy camp represent the number of soldiers stationed in that camp.

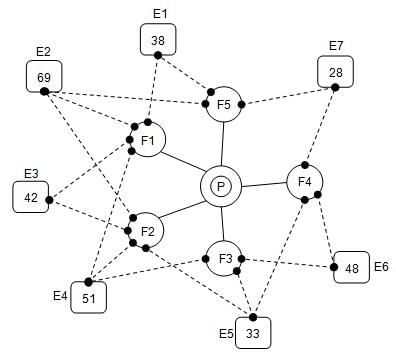
Assume that all the Bagami soldiers attack the fortifications that they are assigned to at the same time and each soldier will attack exactly one fortification. Also, a higher numerical strength in terms of soldiers will assure victory to any side in such a manner that, if, say, 10 Bagami soldiers attack a fortification with 11 Alami soldiers, all the Bagami soldiers will die and the fortification will remain safe, but with only 1 Alami soldier remaining alive. If the number of Bagami soldiers attacking a fortification is equal to the number of Alami soldiers at the fortification, all the soldiers belonging to both the sides will die but the fortification will remain safe. In a similar manner, if the number of Bagami soldiers attacking is in excess of the number of Alami soldiers, the fortification will be destroyed, but with only the excess number of Bagami soldiers remaining alive.

Q. If it is known that the Bagami king is planning to send an equal number of soldiers from each enemy camp to all the possible fortifications from that enemy camp, what is the number of soldiers that will be killed during the attack, if no fortification
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 15
The total number of enemy soldiers that will attack the fortifcation = 309 Since the number of soldiers attacking each fortification is already known, the number of Alami soldiers will also be 309. Hence, a minimum of 618 soldiers will die if no fortification is to be destroyed.

CAT DI And LR Mock Test - 2 - Question 16
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

The capital city of the kingdom of Alami has the royal palace in the centre, with five fortifications, labelled F1 to F5, surrounding the palace. All the Alami soldiers are always present at the royal palace unless ordered to move to a fortification. An enemy kingdom Bagami planned to attack the royal palace and built camps around the fortifications. The Bagamis built seven camps - E1 to E7 - around the Alami fortifications and each Bagami camp had a certain number of soldiers. The soldiers from a given Bagami camp can attack only some of the fortifications, as indicated in the diagrambelow. However, all the soldiers from a single Bagami camp need not necessarily attack the same fortification. The Alami king came to know about this and was planning to send his soldiers to the fortifications.

The following diagram shows the royal palace (P), fortifications (F1 to F5) and enemy (Bagami) camps (E1 to E7). The solid lines in the figure represent the respective fortification to which the Alami soldiers can be deployed from the palace. The dotted lines from each enemy camp represent the fortifications that the soldiers from that enemy camp can attack. The numbers inside each enemy camp represent the number of soldiers stationed in that camp.

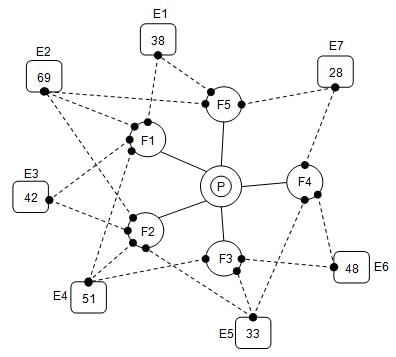
Assume that all the Bagami soldiers attack the fortifications that they are assigned to at the same time and each soldier will attack exactly one fortification. Also, a higher numerical strength in terms of soldiers will assure victory to any side in such a manner that, if, say, 10 Bagami soldiers attack a fortification with 11 Alami soldiers, all the Bagami soldiers will die and the fortification will remain safe, but with only 1 Alami soldier remaining alive. If the number of Bagami soldiers attacking a fortification is equal to the number of Alami soldiers at the fortification, all the soldiers belonging to both the sides will die but the fortification will remain safe. In a similar manner, if the number of Bagami soldiers attacking is in excess of the number of Alami soldiers, the fortification will be destroyed, but with only the excess number of Bagami soldiers remaining alive.

Q. During the attack, if a total of 612 soldiers died on both the sides put together, what is the minimum number of fortifications that would not have been destroyed?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 16
Since a total of 612 soldiers died, 306 form each side would have died. This implies that 3 enemy soldiers are remaining. This means that a maximum of three fortifications (one each) could have been destroyed. Hence, the minimum number of fortifications that would not have been destroyed will be 5 - 3 = 2.

CAT DI And LR Mock Test - 2 - Question 17
Save

DIRECTIONS for questions: Each question is followed by two statements, I and II, giving certain data. You have to decide whether the information provided in the statements is sufficient for answering the question and mark your answer as How many students from the top 20 rankers in the institute are Commerce graduates if it is known that none of the top five rankers are Commerce graduates?

I. None of the last four out of the top 20 rankers are Commerce graduates.

II. At least 8 of the top 15 rankers and not more than 8 of the last fifteen out of 20 top rankers are Commerce graduates.
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 17
The question cannot be answered using statement I alone. From statement n alone we can get the answer. If there are at least eight commerce graduates in the top 15 they must be in the ranks 6 to 15 only (because the top 5 are not commerce graduates). When we consider the last 15 of the top 20, since this will be from 6 to 20, all the eight or more commerce graduates in the ranks 6 to 15 should also be counted here. That means, at least 8 commerce graduates must be there from 6 to 20. But statement n itself says that there are not more than 8 commerce graduates from ranks 6 to 20. This means, there are exactly eight commerce graduates from 6 to 20 or in other words, there are 8 commerce graduates in the top twenty rankers.

CAT DI And LR Mock Test - 2 - Question 18
Save

DIRECTIONS for questions: Each question is followed by two statements, I and II, giving certain data. You have to decide whether the information provided in the statements is sufficient for answering the question and mark your answer as

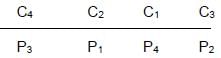
Four cities - C1, C2, C3 and C4 - lie in a straight line, not necessarily in the same order, with the distance between any two adjacent cities being equal. From each of these cities, exactly one person among P1, P2, P3 and P4 starts simultaneously towards one of the other cities. From which city did P4 start?

I. From the starting point of P1, he can reach either of the cities C1 and C4 in the same time.

II. Even if P3 is twice as fast as P2, he cannot reach city C3 by the time P2 reaches the city C1.
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 18
Let the distance between each pair of adjacent cities be x km.

From I, we can only say that the city from which P1 is starting, is equidistant from C1 and C4, which is not sufficient to answer the question.

From II, if there is at least one city between the city from which P2 starts and C1, then by the time P2 reaches C1, P3 must have reached C3, whatever be the position of the cities.

∴C1 is adjacent city to the city from which P2 started.

By the time P2 reaches C1(i.e., by covering x km). P3 would have covered 2x km.

The city from which P3 started and the city C3 must be at the extreme ends.

But we cannot say anything about P4.

∴ II alone is not sufficient. Combining both the statements, as the city from which P2 is started is adjacent to C1, the possible arrangement is as follows.

∴ P4 started from C1.

CAT DI And LR Mock Test - 2 - Question 19
Save

DIRECTIONS for questions: Each question is followed by two statements, I and II, giving certain data. You have to decide whether the information provided in the statements is sufficient for answering the question and mark your answer as At a primary school, girls and boys were going from their morning assembly to their classrooms in separate lines. They had to move through a narrow doorway, where the two lines had to merge into one. After the lines merged, no girl had overtaken any other girl and no boy had overtaken any other boy. Initially, Meena was in the 4th position from the front in the girls line and her brother was at the 6th position from the end in the boys line. If after the lines merged, there were eight students ahead of Meena, how many boys were behind Meena?

I. There were three boys between Meena and her brother.

II. After the merger, Meena was ahead of her brother.
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 19
After the merges, there are 8 students ahead of Meena (M), 3 girls and 5 boys. From I, we have to consider two possibilities. If Meena is ahead of her brother (br), we get

If Meena is behind her brother, we get

∴ There could be 9 boys or 2 boys behind Meena.

II alone is not sufficient.

But along with I, we see that the number of boys behind Meena is 9.

CAT DI And LR Mock Test - 2 - Question 20
Save

DIRECTIONS for questions: Each question is followed by two statements, I and II, giving certain data. You have to decide whether the information provided in the statements is sufficient for answering the question and mark your answer as Vijay bought a new television costing at least Rs.10,000 after exchanging his old television with the new one. If exchanging the old television resulted in a 30% discount in the price of the new television, find the amount Vijay paid for purchasing the new television.

I. He borrowed an amount which was equal to 20% of the cost of the old television from his friend and raised the remaining amount from his personal savings.

II. His total personal savings were Rs.6400.
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 20
Let the cost of the new television be ₹x, then the cost of the old television is ₹0.3x using statement I alone

The amount borrowed by Vijay = ₹0.2 (0.3x) ₹0.06x

The remaining amount required by Vijay is 0.64x which he obtains from his savings. But we cannot determine the cost of the new television.

Hence statement I alone is not sufficient. Using statement n alone we will not be able to answer the question.

By combining both the statements, as the cost of the new television is atleast ₹10,000, he has to use all the money in the savings account and the cost of the new television is exactly ₹10,000.

CAT DI And LR Mock Test - 2 - Question 21
Save

DIRECTIONS for questions: Each question is followed by two statements, I and II, giving certain data. You have to decide whether the information provided in the statements is sufficient for answering the question and mark your answer as How many among the four players - A, B, C and D scored a century?

I. Ram said A and B scored centuries while Mohan said at least two among A, C and D scored centuries.

II. Ram always tells the truth while Mohan always lies.
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 21
Form statement I,

Ram: A, B scored centuries.

Mohan: The group out of A, C, D having scored centuries can be (AC), (AD), (CD) or (A, C, D)

Thus statement (I) alone is not sufficient.

Also, statement (n) alone is not sufficient.

From statement (I) and statement (II) combined, Ram is truth teller.

This implies A and B must have scored centuries Mohan lies.

This implies none or only one person out of A, C, D must have scored centuries.

Already A has scored century. So, C and D must not have scored century.

Both statements together are sufficient.

CAT DI And LR Mock Test - 2 - Question 22
Save

DIRECTIONS for questions: Each question is followed by two statements, I and II, giving certain data. You have to decide whether the information provided in the statements is sufficient for answering the question and mark your answer as I have a total of 125 fruits - apples and oranges put together - which are to be distributed to 12 boys and 9 girls of a class, such that each girl gets at least one apple but no orange but each boy gets at least one apple and at least one orange. Can apples be distributed equally to all the 21 students? Assume that the number of fruits of any variety, distributed for any person is always an integer.

I. The number of apples is a multiple of 7.

II. The oranges can be distributed equally to all the boys.
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 22
From statement I alone, we know that the number of apples is a multiple of seven, but we do not know whether it is a multiple of three or not. So, we cannot find whether it is a multiple of 21 or not.

Hence, statement I alone is not sufficient

From statement II alone, the number of oranges is 12k, where k is a whole number and since total fruits is 125, if there are X apples, X + 12k = 125.

Since 125 is not divisible by 3 and 12k is divisible by 3, X is not divisible by 3. Hence it is not divisible by 21. Hence statement II alone is sufficient.

CAT DI And LR Mock Test - 2 - Question 23
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

Six friends, Das, Kumar, Lal, Ratan, Vinay, and Yuvraj, wanted to play a game of Ludo and decided to draw lots to determine the order in which they play. For this purpose, they took six pieces of paper and wrote down a different number, from 1 to 6, on each piece of paper and then put them all in a bag. Each of them picked a piece of paper from the bag, without peeping into the bag, one after the other. They then saw the numbers that each of them picked and decided the order in which they will play. After they finished the game, they made the following statements, all of which are true:

Das : I picked a number which was greater than the number picked by Lal and the number four was already picked before I picked a number.

Kumar : I was the third person to pick a number and the number two was already picked by that time.

Lal : I picked a number after Ratan did and the number picked by Ratan was lower than mine.

Ratan : I picked a number lower than the number picked by Yuvraj and I picked the number after Das did.

Vinay : Ratan and I picked consecutive numbers and neither of us picked the lowest number.

Yuvraj : I did not pick the highest number and nor was I the first to pick a number.

Q. Which number did Yuvraj pick?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 23
Given that Vinay and Ratan picked consecutive numbers. Also, Ratan picked a number lower than Yuvraj. Yuvraj did not pick the highest number. Yuvraj could have picked a maximum of 5. Hence, Ratan and Vinay could have picked 2 and 3 or 3 and 4.

If Ratan and Vinay picked 3 and 4 in any order, Yuvraj must have picked 5. Lai also picked a number higher than Ratan. Hence, Lai should have picked 6, But Das picked a number higher than Lai. Therefore, this case is not possible,

If Ratan and Vinay picked 2 and 3 in any order, Yuvraj could have picked 4 or 5. Lai also must have picked 4 or 5 and Das must have picked 6 (since Das picked a higher number than Lai), 1 must have been picked by Kumar, If Ratan picked 2, he must have picked the number before Kumar, who was 3rd. Bui Das picked the number before Ratan,

Hence, Das must have picked first or second. But according to Das's statement, 4 was picked before Das picked a number. This is not possible.

Hence, Ratan should have picked 3 and Vinay should have picked 2.

If Lai picked 5, Yuvraj would have picked 4. Das should have picked after Yuvraj, according to Das's statement, Ratan and Lai should have picked after Das. Therefore, Das must have picked 4th,Yuvraj should have picked 2nd (since he couldn't have picked first), Vinay should have picked first. Ratan would have been the 5thto pick a number and Lai would have been the last, If Lai picked 4, Yuvraj would have 5, Lai should have picked 4 before Das. Das picked before Ratan. Ratan picked before Lai. This case is. therefore, not possible.

Hence, the following arrangement is possible.

Yuvraj picked four.

CAT DI And LR Mock Test - 2 - Question 24
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

Six friends, Das, Kumar, Lal, Ratan, Vinay, and Yuvraj, wanted to play a game of Ludo and decided to draw lots to determine the order in which they play. For this purpose, they took six pieces of paper and wrote down a different number, from 1 to 6, on each piece of paper and then put them all in a bag. Each of them picked a piece of paper from the bag, without peeping into the bag, one after the other. They then saw the numbers that each of them picked and decided the order in which they will play. After they finished the game, they made the following statements, all of which are true:

Das : I picked a number which was greater than the number picked by Lal and the number four was already picked before I picked a number.

Kumar : I was the third person to pick a number and the number two was already picked by that time.

Lal : I picked a number after Ratan did and the number picked by Ratan was lower than mine.

Ratan : I picked a number lower than the number picked by Yuvraj and I picked the number after Das did.

Vinay : Ratan and I picked consecutive numbers and neither of us picked the lowest number.

Yuvraj : I did not pick the highest number and nor was I the first to pick a number.

Q. Who was the first person to pick a number?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 24
Given that Vinay and Ratan picked consecutive numbers. Also, Ratan picked a number lower than Yuvraj. Yuvraj did not pick the highest number. Yuvraj could have picked a maximum of 5. Hence, Ratan and Vinay could have picked 2 and 3 or 3 and 4.

If Ratan and Vinay picked 3 and 4 in any order, Yuvraj must have picked 5. Lai also picked a number higher than Ratan. Hence, Lai should have picked 6, But Das picked a number higher than Lai. Therefore, this case is not possible,

If Ratan and Vinay picked 2 and 3 in any order, Yuvraj could have picked 4 or 5. Lai also must have picked 4 or 5 and Das must have picked 6 (since Das picked a higher number than Lai), 1 must have been picked by Kumar, If Ratan picked 2, he must have picked the number before Kumar, who was 3rd. Bui Das picked the number before Ratan,

Hence, Das must have picked first or second. But according to Das's statement, 4 was picked before Das picked a number. This is not possible.

Hence, Ratan should have picked 3 and Vinay should have picked 2.

If Lai picked 5, Yuvraj would have picked 4. Das should have picked after Yuvraj, according to Das's statement, Ratan and Lai should have picked after Das. Therefore, Das must have picked 4th, Yuvraj should have picked 2nd (since he couldn't have picked first), Vinay should have picked first. Ratan would have been the 5th to pick a number and Lai would have been the last, If Lai picked 4, Yuvraj would have 5, Lai should have picked 4 before Das. Das picked before Ratan. Ratan picked before Lai. This case is. therefore, not possible.

Hence, the following arrangement is possible.

Vinay was the first person to pick a number.

CAT DI And LR Mock Test - 2 - Question 25
Save

DIRECTIONS for questions: Answer the questions on the basis of the information given below.

Six friends, Das, Kumar, Lal, Ratan, Vinay, and Yuvraj, wanted to play a game of Ludo and decided to draw lots to determine the order in which they play. For this purpose, they took six pieces of paper and wrote down a different number, from 1 to 6, on each piece of paper and then put them all in a bag. Each of them picked a piece of paper from the bag, without peeping into the bag, one after the other. They then saw the numbers that each of them picked and decided the order in which they will play. After they finished the game, they made the following statements, all of which are true:

Das : I picked a number which was greater than the number picked by Lal and the number four was already picked before I picked a number.

Kumar : I was the third person to pick a number and the number two was already picked by that time.

Lal : I picked a number after Ratan did and the number picked by Ratan was lower than mine.

Ratan : I picked a number lower than the number picked by Yuvraj and I picked the number after Das did.

Vinay : Ratan and I picked consecutive numbers and neither of us picked the lowest number.

Yuvraj : I did not pick the highest number and nor was I the first to pick a number.

Q. Which of the following statements is true?
Detailed Solution for CAT DI And LR Mock Test - 2 - Question 25
Given that Vinay and Ratan picked consecutive numbers. Also, Ratan picked a number lower than Yuvraj. Yuvraj did not pick the highest number. Yuvraj could have picked a maximum of 5. Hence, Ratan and Vinay could have picked 2 and 3 or 3 and 4.

If Ratan and Vinay picked 3 and 4 in any order, Yuvraj must have picked 5. Lai also picked a number higher than Ratan. Hence, Lai should have picked 6, But Das picked a number higher than Lai. Therefore, this case is not possible,

If Ratan and Vinay picked 2 and 3 in any order, Yuvraj could have picked 4 or 5. Lai also must have picked 4 or 5 and Das must have picked 6 (since Das picked a higher number than Lai), 1 must have been picked by Kumar, If Ratan picked 2, he must have picked the number before Kumar, who was 3rd. Bui Das picked the number before Ratan,

Hence, Das must have picked first or second. But according to Das's statement, 4 was picked before Das picked a number. This is not possible.

Hence, Ratan should have picked 3 and Vinay should have picked 2.

If Lai picked 5, Yuvraj would have picked 4. Das should have picked after Yuvraj, according to Das's statement, Ratan and Lai should have picked after Das. Therefore, Das must have picked 4th, Yuvraj should have picked 2nd (since he couldn't have picked first), Vinay should have picked first. Ratan would have been the 5th to pick a number and Lai would have been the last, If Lai picked 4, Yuvraj would have 5, Lai should have picked 4 before Das. Das picked before Ratan. Ratan picked before Lai. This case is. therefore, not possible.

Hence, the following arrangement is possible.

Among the given statements, only the statement given in option C is true.

Information about CAT DI And LR Mock Test - 2 Page
In this test you can find the Exam questions for CAT DI And LR Mock Test - 2 solved & explained in the simplest way possible. Besides giving Questions and answers for CAT DI And LR Mock Test - 2, EduRev gives you an ample number of Online tests for practice

Top Courses for CAT

Download as PDF

Top Courses for CAT

Important Questions for CAT DI And LR Mock Test - 2

Find all the important questions for CAT DI And LR Mock Test - 2 at EduRev.Get fully prepared for CAT DI And LR Mock Test - 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the CAT DI And LR Mock Test - 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of CAT DI And LR Mock Test - 2 resources.

CAT DI And LR Mock Test - 2 MCQs with Answers

Prepare for the CAT DI And LR Mock Test - 2 within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for CAT DI And LR Mock Test - 2

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace CAT DI And LR Mock Test - 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup