CAT Mock Test- 5 - CAT MCQ
30 Questions MCQ Test - CAT Mock Test- 5
Why does the author give the examples of the Santa Susana Lab and Chernobyl?
Which of the following adds the least depth to the author’s argument?
The passage makes all the following claims EXCEPT:
- “Hill-billy” was considered a derogatory word.
- Country music was more progressive than it was perceived to be.
- The audience of country music was diverse.
What is the author is trying to do by citing the example of Loretta Lynn?
Which of the following statements can be inferred from the passage?
What is the author most likely to discuss after the final paragraph?
Which of the following can be inferred about Asa Gray?
I: He studied at Cambridge University
II: He was a writer
III: He was an editor
IV: He was a confidant of the editors of the journal from which the article is taken
Which of the following is not an aspect of Asa Gray’s written work?
Which of the following best explains the reason behind the author stating Asa Gray as less fortunate than George Bentham?
Four sentences are given below. These sentences, when rearranged in proper order, form a logical and meaningful paragraph. Rearrange the sentences and enter the correct order as the answer.
- Wherever the rhythm was most delicate, wherever the emotion was most ecstatic, her art was the most beautiful, and yet, although she sometimes spoke to a little tune, it was never singing, as we sing to-day, never anything but speech.
- I have always known that there was something I disliked about singing, and I naturally dislike print and paper, but now at last I understand why, for I have found something better.
- A friend, who was here a few minutes ago, has sat with a beautiful stringed instrument upon her knee, her fingers passing over the strings, and has spoken to me some verses from Shelley’s Skylark and Sir Ector’s lamentation over the dead Launcelot out of the Morte d’Arthur and some of my own poems.
- I have just heard a poem spoken with so delicate a sense of its rhythm, with so perfect a respect for its meaning, that if I were a wise man and could persuade a few people to learn the art I would never open a book of verses again.
Five sentences are given below. Four of which when arranged in a proper order, form a logical and meaningful paragraph. Identify the sentence that does not belong to the paragraph and enter its number as your answer.
- With the modern tendency toward specialization, the natural outgrowth of necessity, there is no inherent reason why the bones of a building should not be devised by one man and its fleshly clothing by another, so long as they understand one another, and are in ideal agreement, but there is in general all too little understanding, and a confusion of ideas and aims.
- Preoccupied as he is with the building's strength, safety, economy; solving new and staggeringly difficult problems with address and daring, he has scant sympathy with such inconsequent matters as the stylistic purity of a façade, or the profile of a moulding.
- To the designer, on the other hand, the engineer appears in the light of a subordinate to be used for the promotion of his own ends, or an evil to be endured as an interference with those ends.
- In the field of domestic architecture these dramatic contrasts are less evident, less sharply marked.
- To the average structural engineer the architectural designer is a mere milliner in stone, informed in those prevailing architectural fashions of which he himself knows little and cares less.
Five sentences are given below labelled as 1, 2, 3, 4 and 5. Of these, four sentences, when arranged properly, make a meaningful and coherent paragraph. Identify the odd one out.
- Even where the advancer of the art was also a psychologist, the pedagogics and the psychology ran side by side, and the former was not derived in any sense from the latter.
- To know psychology, therefore, is absolutely no guarantee that we shall be good teachers.
- The art of teaching grew up in the schoolroom, out of inventiveness and sympathetic concrete observation.
- That ingenuity in meeting and pursuing the pupil, that tact for the concrete situation, though they are the alpha and omega of the teacher's art, are things to which psychology cannot help us in the least.
- The two were congruent, but neither was subordinate.
The four sentences (labelled 1, 2, 3, and 4) below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. Yet, its implications in disrupting traditional power structures are often grossly underestimated.
2. The digital revolution, much like previous revolutions, has been a source of profound economic and social transformation.
3. Historically, revolutions have redefined space for innovation and freedom, creating unforeseen opportunities for decentralization.
4. Conversely, it opens a Pandora's Box of heightened surveillance, control, and societal imbalance, overshadowing its emancipatory potential.
The four sentences (labelled 1, 2, 3, and 4) below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
1. This shift necessitates an interrogation of traditional economic models, demanding innovative perspectives on wealth and productivity.
2. As automation and artificial intelligence take center stage, the global workforce faces unprecedented transformation.
3. Thus, nations grapple with the intricacies of integrating rapidly evolving technology into an already fragile global economy.
4. Interestingly, these advancements could herald a new era where human potential is optimized, redefining conventional work boundaries.
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
In the last two decades, the phenomenon of 'digital nomads' has emerged, signifying a deeper change in conceptions of work and life. These individuals leverage technology to work remotely, often traveling globally. While this lifestyle offers unprecedented freedom and flexibility, it also entails significant downsides. Digital nomads frequently face issues related to psychological isolation, unpredictable finances, and the absence of a stable community. This lifestyle, embodying a post-modernist rebellion against traditional 9-5 jobs, questions the very fabric of societal norms but also underscores the human yearning for connection, stability, and security.
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
Artificial intelligence (AI) in healthcare is a revolutionary force, with the potential to significantly cut costs and improve patient outcomes. By analyzing vast datasets beyond human capability, AI can identify patterns and predictions invaluable for diagnosis and treatment strategies. However, this innovation comes with caveats. Concerns about data privacy, algorithm biases, and a potential decrease in face-to-face patient care necessitate careful integration of AI, with an emphasis on ethics and quality of human interaction to complement technological prowess.
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
Climate change-induced migration is becoming a stark reality. As habitats become inhospitable, mass movements of populations are causing geopolitical tensions. Wealthier nations are building barriers, both legal and physical, against migrants whom they perceive as threats to economic stability and social identity. This approach is short-sighted, ignoring the shared responsibility of humankind in climate change and the universal rights of those displaced. A more humane and sustainable approach would be global cooperation towards climate solutions, acknowledging the interconnectedness of our environmental actions.
If it is known that the total number of people in the sports club were 2300 and out of them, only 395 followed none of the clubs, what can be the maximum number of people who follow exactly 3 clubs?
If the following data is additionally given, which of the following can be a possible number of people who followed all but CSK?
- Every person follows at least one club.
- No person follows exactly 2 clubs.
- The number of persons who follow all but RCB is 49.
- The number of persons who follow all but SRH is 53.
- The number of persons who follow all but KKR is 37.
- The total number of people in the sports club is 1307.
If the total number of people in the sports club is 1306, and everyone follows a minimum of one of the four clubs and the number of people who support all 4 clubs is the maximum, what is the ratio of the number of people who follow only RCB to those who follow only SRH?
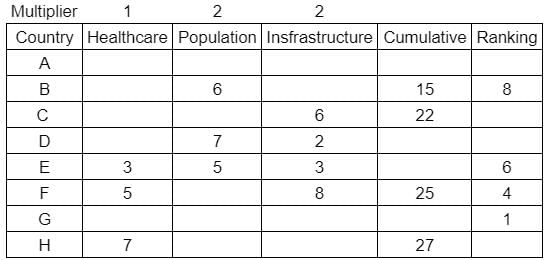
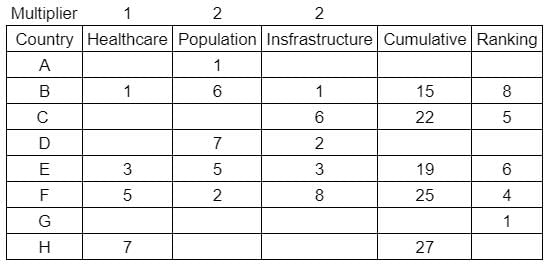
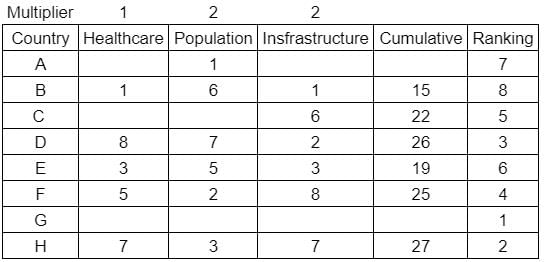
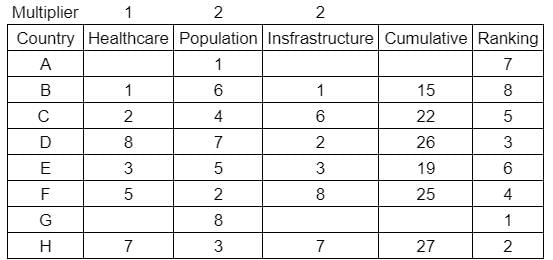
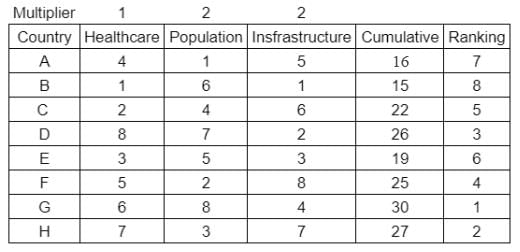
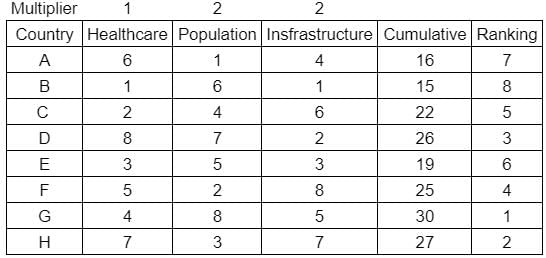
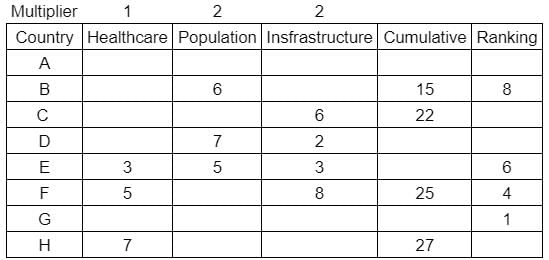
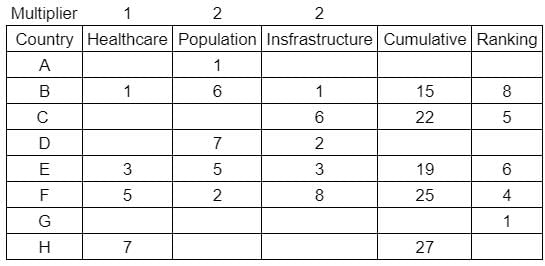
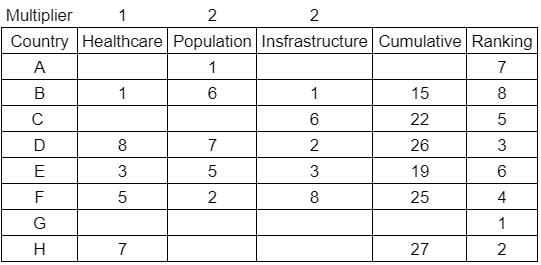
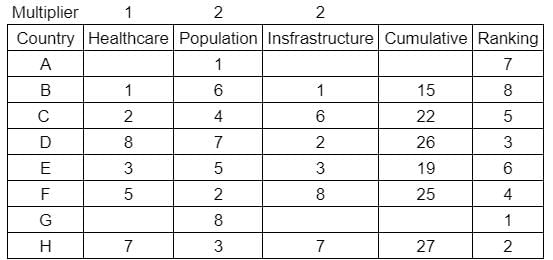
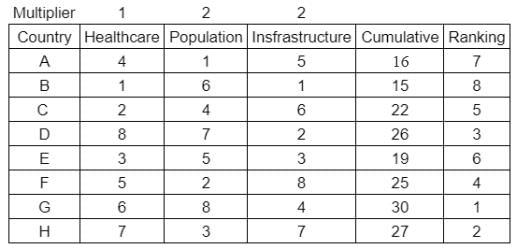
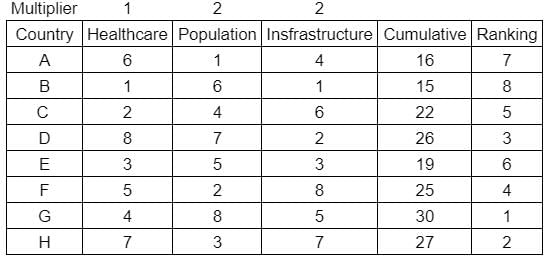
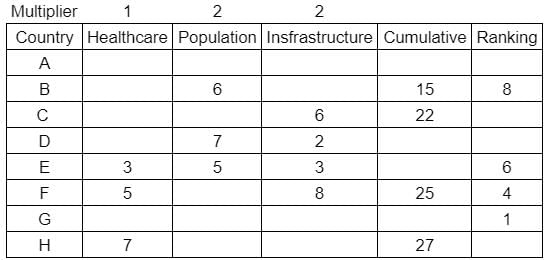
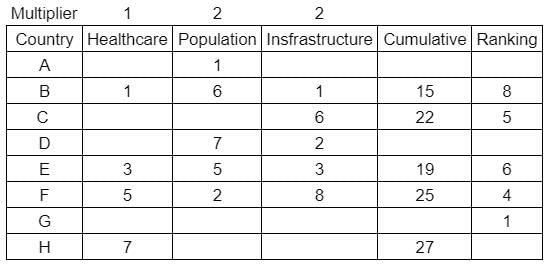
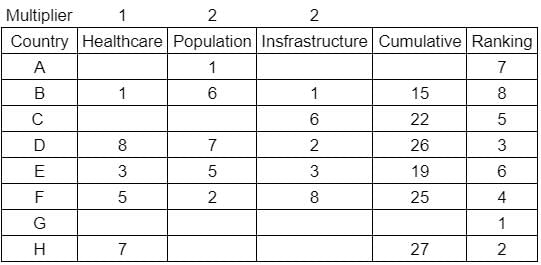
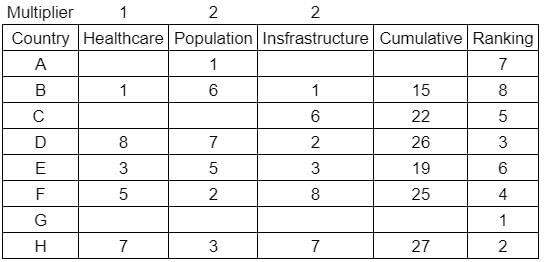
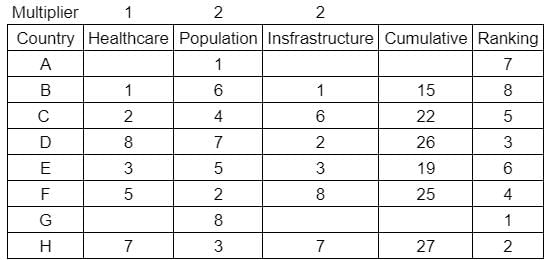
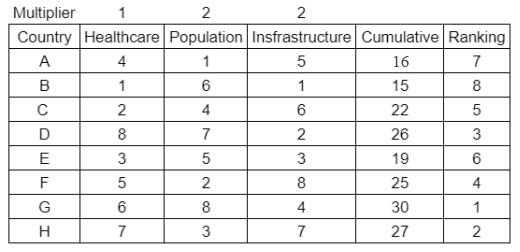
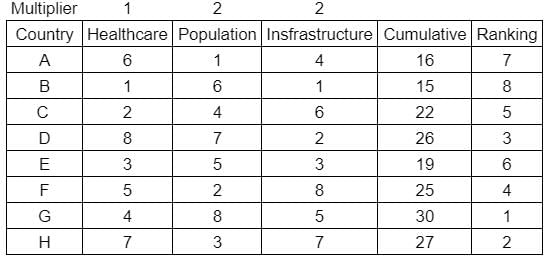
What is rank of country C?
Enter -1 if the answer can't be determined.