CSIR NET Mathematical Science Mock Test - 8 - UGC NET MCQ
30 Questions MCQ Test CSIR NET Exam Mock Test Series 2025 - CSIR NET Mathematical Science Mock Test - 8
A person bought an article and sold it at a loss of 10%. If he had bought for 20% less and sold it for Rs.55 more, he would have had a profit of 40%. Then what is the cost price of the article?
Which of the following steps are required to design a questionnaire?
1. Writing primary and secondary aims of the study.
2. Review of the current literature.
3. Prepare a draft of questionnaire.
4. Revision of the draft.
Select the correct answer from the codes given below:
A man wills 40% of his wealth to his wife and rest to orphans. What percent of the wealth willed the orphans get more than his wife?
Company 'x' manufactures watches. The manufacturing cost is 40%, tax is 10% and 50% is their profit. If the manufacturing cost increases by 10% and tax by 1%, then the cost of watch has to be increased by 82 rupees to get the same profit amount. What is the amount of profit they can make per piece of watch?
Directions: What will come in place of the question mark (?) in the following number series?
6, 42, 163, 419, ?
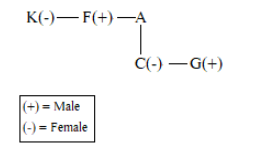
F is the brother of A. C is the daughter of A. K is the sister of F, G is the brother of C. who is the uncle of G ?
If ai, bi; and ci are distinct, how many terms will the expansion of the product (a1 + a2 + a3) (b1 + b2 + b3 + b4) (c1 + c2 + c3 + c4 + c5) contain?
The equation of the curve whose sub normal is equal to a constant a is —
Solve the following differential equation:

What is the Cardinality of the Power set of the set {0, 1, 2}?
The derivative of the function f(x) = x2m is—
The derivative of the function f(x) = sin n x is—
The radius of convergence of the series 1 – x2 + x4 – x6 + …… is—
In a hypothesis-testing problem, which of the following is not required in order to compute the p-value ?
Let f : [0, 1] → [0, 1] be any twice differentiable function satisfyingf (ax + (1 – a) y) ≤ af (x) + (1 – a) f (y) for all x, y ∈ [0, 1] and any a ∈ [0, 1]. Then for all x ∈ (0, 1)—
If A is open set and B is closed set,
(A) A – B is open set
(B) A – B is closed set
(C) B – A is open set
(D) B – A is closed set
If K is a compact metric space and 〈 fn〉 an equicontinuous sequence of functions to a metric space Y that converges at each point of K to a function f.
If 〈 fn 〉 is an equicontinuous sequence of mappings from a metric space X to a complete metric space Y. If the sequences 〈 fn(x)〉 converge for each point x of a dense subset D of X,
Let X1, …, Xn be independent and identically distributed random variables with probability density function—
f(x) = 1/2 λ3x2e–λx; x > 0, λ > 0 Then which of the following statements are true ?
A linear operator T on a complex vector space V has characteristic polynomial x3(x – 5)2 and minimal polynomial x3(x – 5). Choose all correct options—
Let X1 and X2 be independent random variables with cumulative distribution functions (cdf) F1 and F2 respectively. Let G be the cdf of X1 + X2 and H be the cdf of X1X2. Identify the correct statements—
Let {an}n ≥ 1 be a sequence of positive numbers such that a1 > a2 > a3 > … Then which of the following is/are always true ?


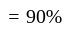 of
of 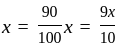
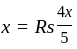
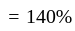 of
of 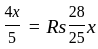
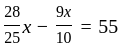
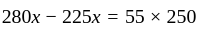


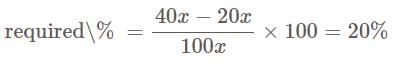
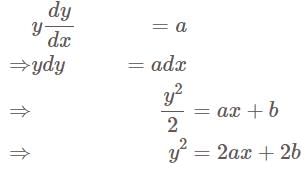



 and
and 
 becomes,
becomes, 






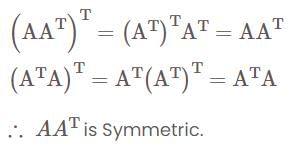
 is
is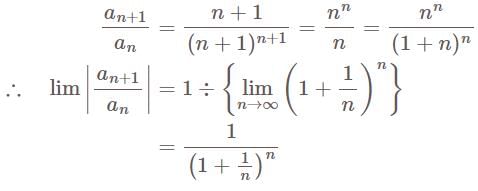




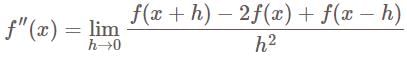
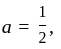 we have
we have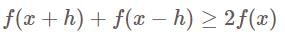
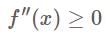
 .
.




 ......(1)
......(1) , i.e. at
, i.e. at  , putting this in (1),
, putting this in (1),

 in (1), we get:
in (1), we get:




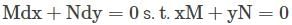 then general solution of
then general solution of 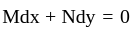 is
is
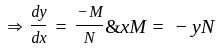
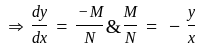
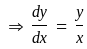
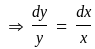
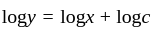
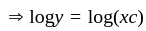
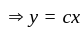
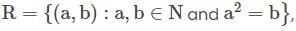 then what is the relation of R?
then what is the relation of R?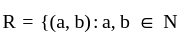 and
and 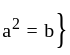
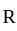 is not reflexive since,
is not reflexive since, 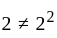
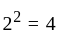 so,
so, 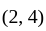 belong to
belong to 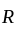
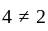 and so,
and so, 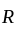 is not symmetric
is not symmetric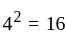 , so
, so 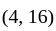 belong to
belong to 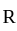
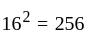 , so
, so 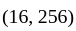 belong to
belong to 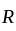
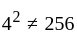 so
so  is not transitive
is not transitive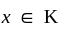 is contained in an open set
is contained in an open set 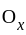 such that
such that 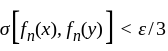 for all
for all 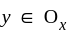 and all
and all 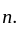 Form this it also follows that
Form this it also follows that 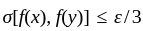 for all
for all 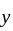 in
in 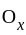
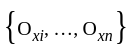 of these sets which covers k
of these sets which covers k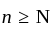 we have
we have 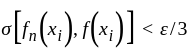 for each
for each 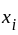 corresponding to this finite collection. Then for any
corresponding to this finite collection. Then for any 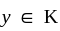 there is an
there is an 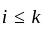 such that
such that 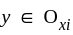 . Hence
. Hence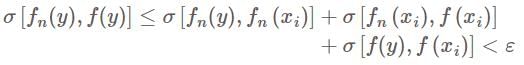 for
for 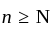 . Thus
. Thus 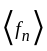 converges to f uniformly on k
converges to f uniformly on k

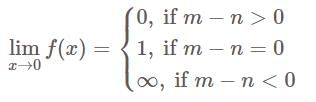
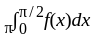 is a proper integral if
is a proper integral if 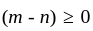 , and improper if
, and improper if 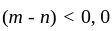 being the only point of infinite discontinuity of the integrand in this case.
being the only point of infinite discontinuity of the integrand in this case.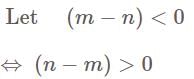
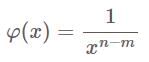
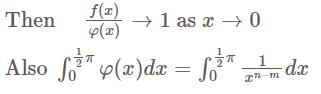
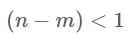
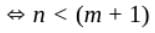
 converges if and only if
converges if and only if 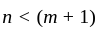 , which also includes the case
, which also includes the case 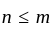 when the integral is proper.
when the integral is proper.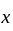 in
in 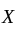 and
and 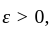 we can find an open set
we can find an open set 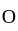 containing
containing 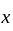 such that
such that 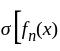
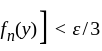 for all
for all 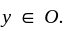 since D is dense, there must be a point
since D is dense, there must be a point 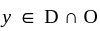 and
and 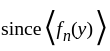 converges, so it must be a Cauchy sequence, so for
converges, so it must be a Cauchy sequence, so for 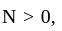 we have
we have 
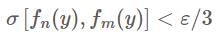
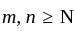
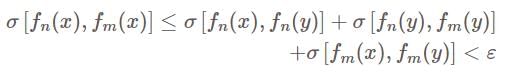
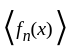 is a Cauchy sequence and converges by the completeness of Y
is a Cauchy sequence and converges by the completeness of Y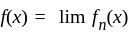 . To prove
. To prove 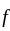 is continuous at
is continuous at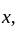 let
let 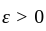 be given. By equicontinuity there is an open set
be given. By equicontinuity there is an open set 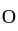 containing
containing 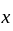 such that
such that 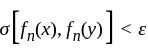 for all
for all 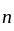 and all
and all 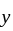 in
in 
 in
in  we have
we have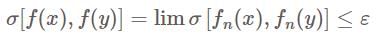 and f is continuous at x
and f is continuous at x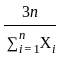 is a consistent estimator of
is a consistent estimator of 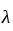

 we have
we have 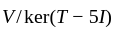 naturally isomorphic to
naturally isomorphic to 
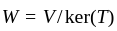 , the induced operator
, the induced operator 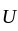 on
on 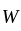 has
has 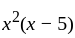 as its minimal polynomial which implies (4) is false. We can see this by considering the Jordan form of
as its minimal polynomial which implies (4) is false. We can see this by considering the Jordan form of  (It's the lower right
(It's the lower right  submatrix of the above matrix.) Alternatively, let
submatrix of the above matrix.) Alternatively, let 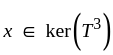
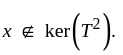 Then
Then 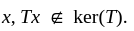 If we let
If we let 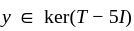 , then
, then 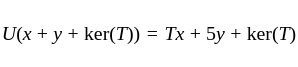
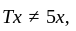 we again have that (4) is false.
we again have that (4) is false.















