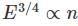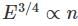CSIR NET Physical Science Mock Test - 2 - UGC NET MCQ
30 Questions MCQ Test CSIR NET Exam Mock Test Series 2025 - CSIR NET Physical Science Mock Test - 2
Which one set of letters when sequentially placed at a gap in the given letter series shall complete it.
__nmmn__mmnn__mnnm__
Direction: In each of the following question, select the one which is different from the others.
(a) (12−144)
(b) (13−156)
(c) (14−166)
(d) (15−180)
A bag contains 8 red balls and 12 blue balls. One ball Is drawn at random and replaced with 5 green balls. A second ball was drawn without replacement. What Is the probability that first ball drawn is red In colour and the second ball drawn Is blue in colour?
Today is Monday. What day will it be after 61 days?
In the figure shown above, PQRS is a square. The shaded portion is formed by the intersection of sectors of circles with radius equal to the side of the square and centrs at S and Q.
The probability that any point picked randomly within the square falls in the shaded area is ________
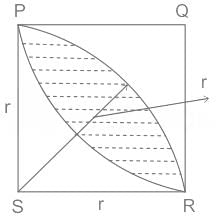
The total expenditure of a family, on different activities in a month, is shown in the pie-chart. The extra money spent on education as compared to transport (in percent) is ____
Two pipes A and B can fill a tank in 15 minutes and 20 minutes respectively. Both the pipes are opened together but after 4 minutes, pipe A is turned off. What is the total time required to fill the tank?
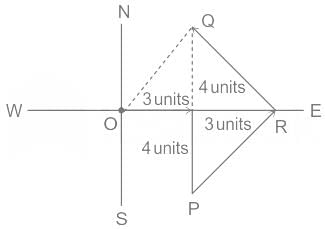
On a planar field, you travelled 3 units East from a point O. Next you travelled 4 units South to arrive at point P. Then you travelled from P in the North-East direction such that you arrive at a point that is 6 units East of point O. Next, you travelled in the North-West direction, so that you arrive at point Q that is 8 units North of point P.
The distance of point Q to point O, in the same units, should be ____
Which of the following inferences can be drawn from the above graph?
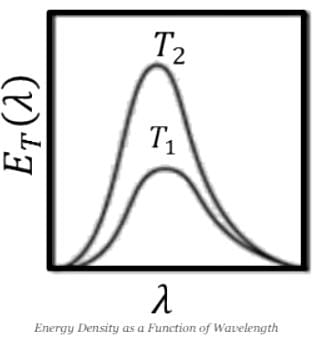
Which of the graphs below gives the correct qualitative behavior of the energy density ET(α) of black body radiation of wavelength λ at two temperature T1 and T2(T1)
Let 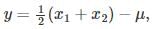 where x1 and x2 are independent and identically distributed Gaussian random variable of mean μ and standard deviation σ. Then
where x1 and x2 are independent and identically distributed Gaussian random variable of mean μ and standard deviation σ. Then 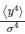 is
is
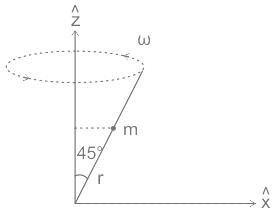
A bead of mass m can slide without friction along a massless rod kept at 45° with the vertical as shown in the figure. The rod is rotating about the vertical axis with a constant angular speed ω. At any instant r is the distance of the bead from the origin. The momentum conjugate to r is?
The Lagrangian of a system is given by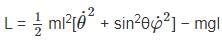 cos θ, where m, l and g are constants.
cos θ, where m, l and g are constants.
Which of the following is conserved?
The acceleration due to gravity (g) on the surface of the earth is approximately 2.6 times that on the surface of the Mars. Given that the radius of the Mars is about one half the radius of the Earth, the ratio of the escape velocity on the Mars to that on the Earth is approximately?
A system has two normal modes of vibration, with frequencies ω1 and ω2=2ω1. What is the probability that at temperature T, the system has an energy less than 4ℎω1? [In the following x=e−βℎω1 and Z is the partition function of the system
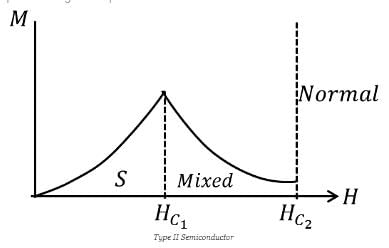
A flux quantum (fluxoid) is approximately equal to 2×10−7 gauss −cm2. A type II superconductor is placed in a small magnetic field, which is then slowly increased till the field starts penetrating the superconductor. The strength of the field at this point is 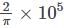 gauss. The penetrate depth of this superconductor is -
gauss. The penetrate depth of this superconductor is -
Consider a particle in a one-dimensional infinite potential well with its wall at x=0 and x=L. The system is perturbed as shown in the following figure.
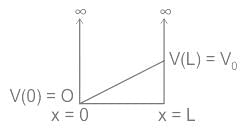
The first-order correction to energy eigenvalue is?
A two-state quantum system has energy eigenvalues is ±ϵ corresponding to the normalized states 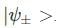 At time t=0, the system is in quantum state
At time t=0, the system is in quantum state 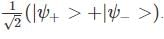 The probability that the system will be in the same state at t = h/6∈ is
The probability that the system will be in the same state at t = h/6∈ is
A frictionless heat-conducting piston of negligible mass and heat capacity divides a vertical, insulated cylinder of height 2H and cross-sectional area A into two halves. Each half contains one mole of an ideal gas at temperatures T0 and P0 corresponding to STP. The heat capacity ratio γ = Cp/Cv is given. A load of weight W is tied to the piston and suddenly released. After the system comes to equilibrium, the piston is at rest and the temperatures of the gases in the two compartments are equal. What is the final displacement y of the piston from its initial position, assuming yW >> T0Cv.
A sample of a substance undergoes a first-order phase transition from a liquid to a solid state. The heat capacity of the substance is given by: Cp = a + bT + cT², where a, b, and c are constants, and T is the temperature. The enthalpy of fusion of the substance is ΔHf = 200 kJ/mol, and its melting point is 300 K. At a pressure of 1 atm, the substance begins to freeze at a temperature of 310 K, and the process is complete at a temperature of 300 K. Calculate the entropy change (ΔS) and the Gibbs free energy change (ΔG) for the freezing process.
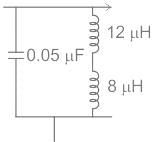
The frequency of the following Hartley oscillator

is nearly equal to :
In a p-type semiconductor, the Fermi level lies 0.4 eV above the valence band. If the concentration of the acceptor atoms is trippled and kT = 0.03 eV, the new position of the Fermi level will be :
The vibrational motion of a diatomic molecule may be considered to be that of a simple harmonic oscillator with angular frequency ω. If a gas of these molecules is at a temperature T, what is the probability that a randomly picked molecule will be found in its lowest vibrational state?
In a spectrum resulting from Raman scattering, let IR denote the intensity of Rayleigh scattering and IS and IAS denote the most intense stokes line and the most intense anti-stokes line, respectively. The order of the intensities are:
The phonon dispersion for the following one-dimensional diatomic lattice with masses M1 and M2 (as shown in the figure)

is given by

where a is the lattice parameter and K is the spring constant. The velocity of sound is
If the Bohr radius is a0, the most probable value of r in the ground state  of Hydrogen atom is
of Hydrogen atom is
A particle with a rest mass of 2 GeV/c2 is accelerated to a speed of 0.8c. Can this moving object displace a particle bound with 4GeV of energy?
We have 238U which decays with a half-life of 4.51 X 105 years, the decay series eventually ending as 206Pb, which is stable. A rock sample analysis shows that the ratio of the number of atoms of 206Pb to 238U is 0.003. Assuming that all the Pb has been produced by the decay of U and that all other half-lives in the chain are negligible. The age of the rock sample is? Given that [ln (1.003) = 0.003]
A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For large n the quantized energy En depends on n as:


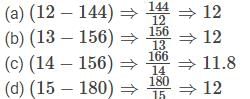

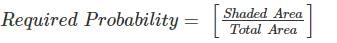
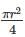
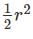
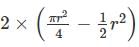
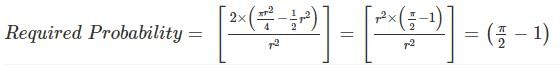
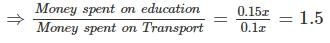
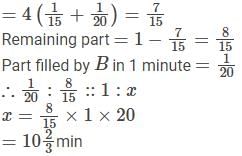
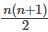 series summation
series summation
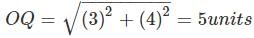
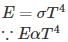
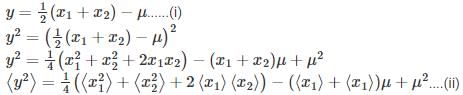

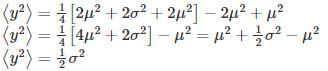
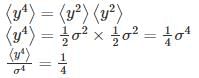
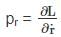
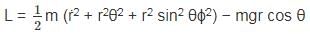
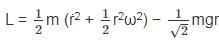
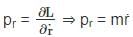
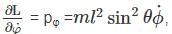 is a constant since m, l and g are constants.
is a constant since m, l and g are constants.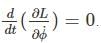
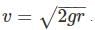 We have to take the ratio of Mars to that of earth we get:
We have to take the ratio of Mars to that of earth we get: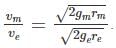 Putting all the given value we get the ratio to be =
Putting all the given value we get the ratio to be = 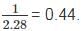
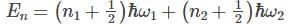
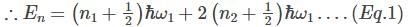
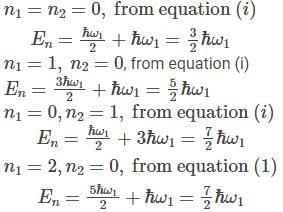
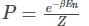
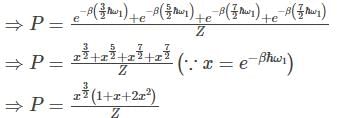
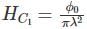
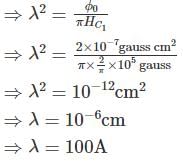
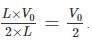
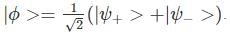
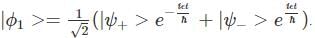
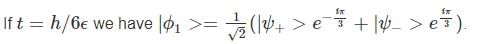
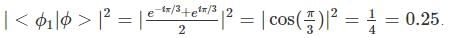
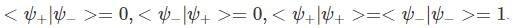
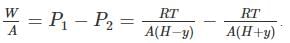
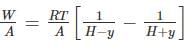
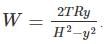
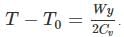
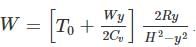
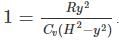

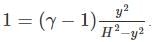
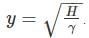
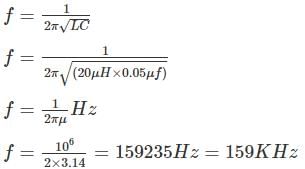
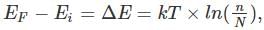 where n is the concentration of free carriers (holes in valence band for p-type), N is the concentration of dopants (acceptor atoms for p-type), kB is Boltzmann's constant, T is the absolute temperature.
where n is the concentration of free carriers (holes in valence band for p-type), N is the concentration of dopants (acceptor atoms for p-type), kB is Boltzmann's constant, T is the absolute temperature.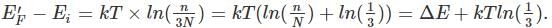
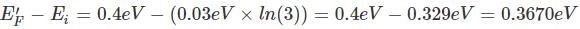


 is the Planck constant.
is the Planck constant.












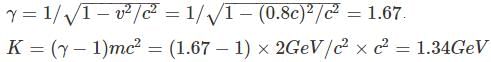
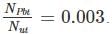 Also as the number of other particles produced in the chain is negligible we have:
Also as the number of other particles produced in the chain is negligible we have: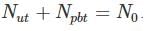
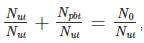 which implies,
which implies,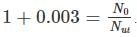
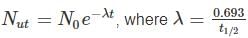 is the decay constant.
is the decay constant.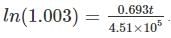
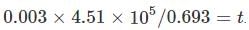
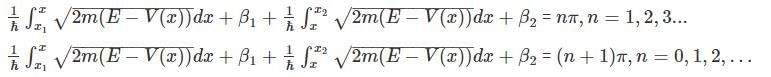
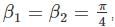 for V (x) to be finite a boundary and
for V (x) to be finite a boundary and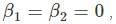 for V(x) to be infinite at the boundary.
for V(x) to be infinite at the boundary.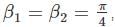 as the potential is finite at the turning points, and we get:
as the potential is finite at the turning points, and we get: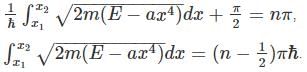
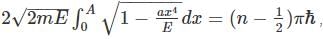 where A is some constant
where A is some constant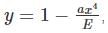 we get:
we get: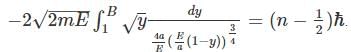
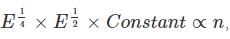 This constant carries a constant after doing the integration.
This constant carries a constant after doing the integration.