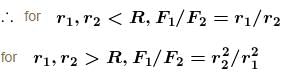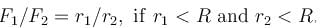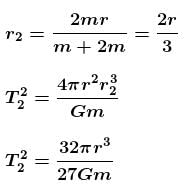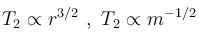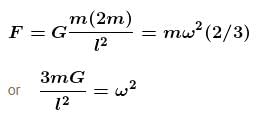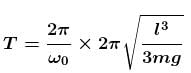Central Forces MSQ - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Central Forces MSQ
Three point masses, m each are at the corners of an equilateral triangle of side a. Their separations do not change when the system rotates about the centre of the triangle. For this, the time period of rotation must be proportional to :
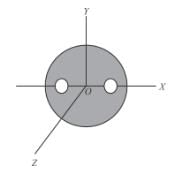
A solid sphere of uniform density and radius 4units is located with its centre at the origin of coordinates, O. Two spheres of equal radii of 1unit, with their centres at A(-2,0,0) and B(2, 0, 0) respectively, are taken out of the solid sphere, leaving behind spherical cavities as shown in the figure.

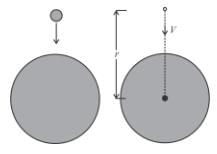
A satellite revolves around a planet in circular orbit of radius R (much larger than the radius of the planet) with a time period of revolution T. If the satellite is stopped and then released in its orbits (Assume that the satellite experiences gravitational force due to the planet only).
Let V and E denotes the gravitational potential and gravitational field at the point. It is possible to have :
A small mass m is moved slowly from the surface of the earth to a height h above the surface. The work done (by an external agent) in doing this is :
A satellite close to the earth is in orbit above the equator with the period of rotation of 1.5hours. If it is above a point P on the equator at some time, it will be above P again after time :
The magnitudes of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively. Then :
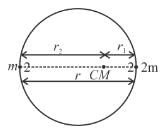
A double star is a system of two stars of masses m and 2m, rotating about their centre of mass only under their mutual gravitational attraction. If r is the separation between these two stars then their time period of rotation about their centre of mass will be proportional to :
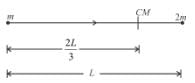
A binary star is a system of two stars rotating about their centre of mass only under their mutual gravitational attraction. Let the stars have masses m and 2m and let their separation be l. Their time period of rotation about their centre of mass will be proportional to :
An object is weighed at the North Pole by a beam balance and a spring balance, giving readings of WB and WS respectively. It is again weighted in the same manner at the equator, giving readings of W′B and W′S respectively. Assume that the acceleration due to gravity is the same everywhere and that the balances are quite sensitive.



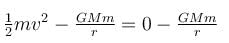
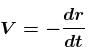
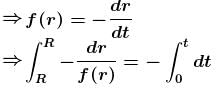
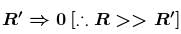
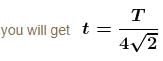

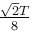
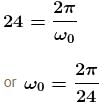
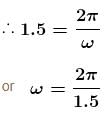
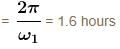
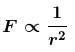 if r > R.
if r > R.