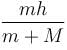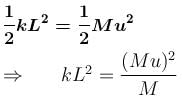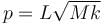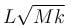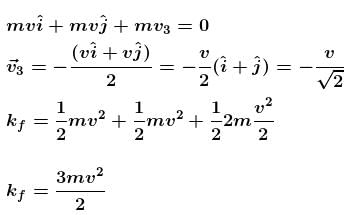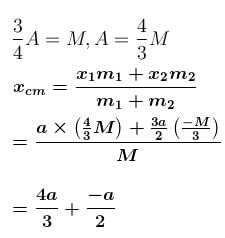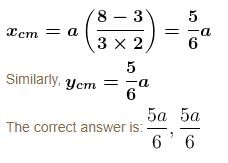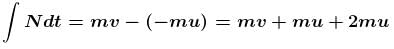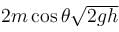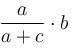Centre Of Mass MCQ Level - 1 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Centre Of Mass MCQ Level - 1
A particle of mass m moving with velocity u1 collides elastically with another particle of same mass moving with velocity u2 in the same direction. After collision their speeds are v1 and v2 respectively then
(A) u1 + v1 = v2 + u2
(B) u1 – v1 = v2 + u2
(A) u1 + v1 = v2 + u2
(B) u1 – v1 = v2 + u2
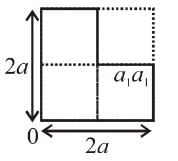
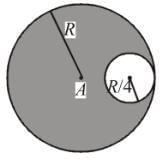
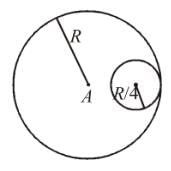
The centre of the mass of the shaded portion of the disc is : (The mass is uniformly distributed in the shaded portion) :

A man of mass M hanging with a light rope which is connected with a balloon of mass m. The system is at rest in air. When man rises a distance h with respect to balloon. Find the distance raised by man :
The block of mass M moving on the frictionless horizontal surface collides with the spring of spring constant k and compresses it by length L. The maximum momentum of the block after collision is :
A particle of mass 4m which is at rest explodes into three fragments. Two of the fragments each of mass m are found to move with a speed v each in mutually perpendicular directions. The minimum energy released in the process of explosion is :
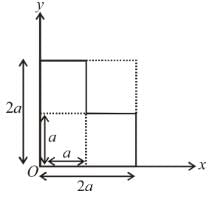
Find the position of centre of mass of the uniform planar sheet shown in figure with respect to the origin (O) :
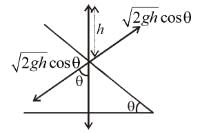
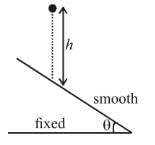
A ball of mass m strikes the fixed inclined plane after falling through a height h. If it rebounds elastically, the impulse on the ball is :
The spacecraft of mass M moves with velocity V in free space at first, then it explodes breaking into two pieces. If after explosion a piece of mass m comes to rest, the other piece of space craft will have :
A ball impinges directly on a similar ball at rest. The first ball is brought to rest by the impact. If half the kinetic energy is lost by impact. What is the value of the coefficient of restitution?
A bullet of mass a and velocity b is fired into a large block of mass c. The final velocity of the system is :


 (For elastic collision e = 1)
(For elastic collision e = 1)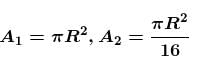
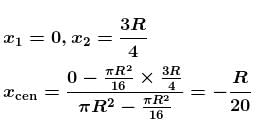

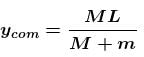
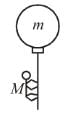
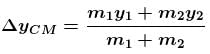
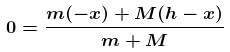
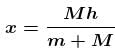 (Distance descend by balloon)
(Distance descend by balloon)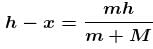 (Distance raised by man)
(Distance raised by man)