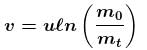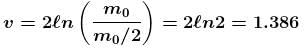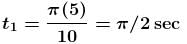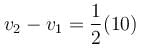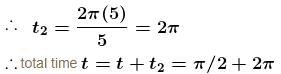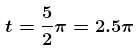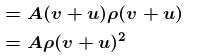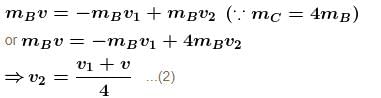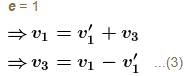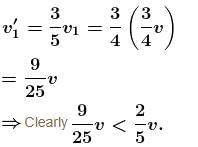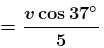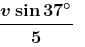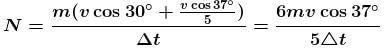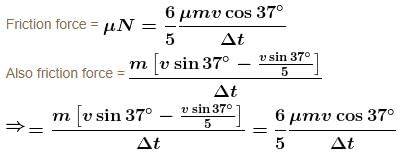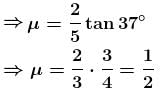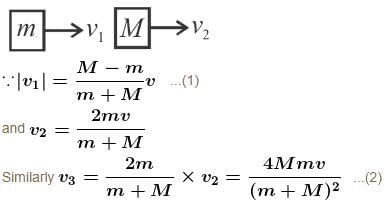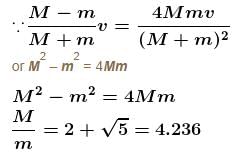Centre Of Mass NAT Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Centre Of Mass NAT Level - 2
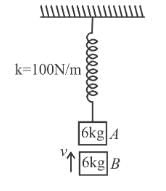
Block A is hanging from a vertical spring and it at rest. Block B strikes the block A with velocity v and sticks to it. The the value of v in m/s for which the spring just attains natural length is :

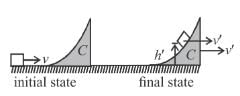
In the figure shown a small block B of mass m is released from the top of a smooth movable wedge A of the same mass m. The height of wedge A shown in figure is h = 100cm. B ascends another movable smooth wedge C of the same mass. Neglecting friction any where find the maximum height (in cm) attained by block B on wedge C.


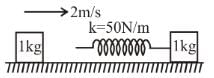
Each of the block shown in figure has mass 1 kg. The near block moves with a speed of 2 m/s towards the front block kept at rest. The spring attached to the front block is light and has a spring constant 50 N/m. Find the maximum compression of the spring. (in cm) :

A stationary body explodes into four identical fragments such that three of them fly off mutually perpendicular to each other, each with same kinetic energy., E0. The energy of explosion is given by nE0. Find the value of n.
A balloon having mass m is filled with gas and is held in hands of a boy. Then suddenly it get released and gas start coming out of it with a constant rate. The velocities of the ejected gases is also constant 2m/s with respect to the balloon. Find out the velocity of the balloon when the mass of gas is reduced to half. [Effect of atmosphere and gravity is neglected]
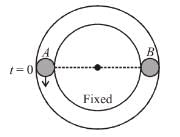
Particle A moves with speed 10 m/s in a frictionless circular fixed horizontal pipe of radius 5 m and strikes with B of double mass that of A. Coefficient of restitution is 1/2 and particle A starts its journey at t = 0. The time at which second collision occurs is given by nπ sec. Find the value of n.
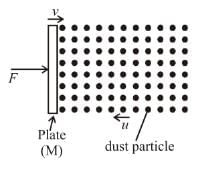
A plate of mass M is moved with constant velocity v against dust particles moving with velocity u in opposite direction as shown. The density of the dust is ρ and plate area is A. Find the force F required to keep the plate moving uniformly is Aρ(u + v)N, then N is :
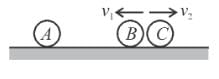
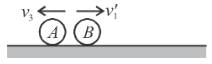
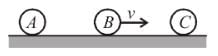
Three ball A, B and C (mA = mC = 4 mB) are placed on a smooth horizontal surface. Ball B collides with ball C with an initial velocity v as shown in the figure. Total number of collision between the balls will be : (All collisions are elastic)
A particle moving on a smooth horizontal surface strikes a stationary wall. The angle of strikes is equal to the angle of rebound and is equal to 37° and the coefficient of restitution with wall is e = 1/5. Find the friction coefficient between wall and the particle in the form X/10. What is the value of X.

Three blocks are placed on smooth horizontal surface and lie on same horizontal straight line. Block 1 and block 3 have mass m each and block 2 has mass M(M > m). Block 2 and block 3 are initially stationary, while block 1 is initially moving towards block 2 with speed v as shown. Assume that all collisions are headon and perfectly elastic. What value of M/m ensures that block 1 and block 3 have the same final speed?
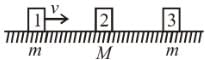



 (see figure.) and comes to rest.
(see figure.) and comes to rest.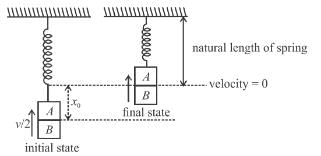
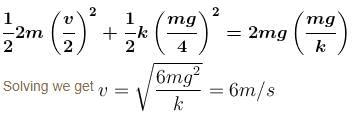



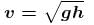 ...(3)
...(3)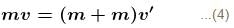

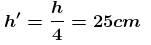

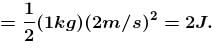
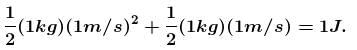
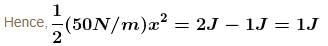

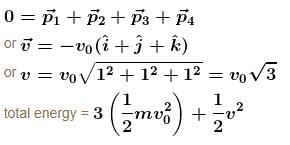 = 3E0 + 3E0
= 3E0 + 3E0