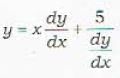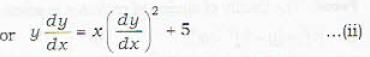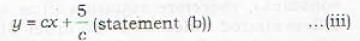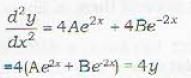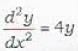Differential Equations - 15 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Differential Equations - 15
Which one of the following is an ordinary differential equation?
The order of the differential equation is defined as the
Which of the following differential equations is of order three?
Which of the following differential equations is of order one?
The degree of a differential equation is defined as the
Let m be the order of a given differential equation. Then
Which of the following differential equations is not of degree 1?
If n denotes the degree of a given differential equation, then
What is the degree of the differential equation, x3 - 6x3 y3 + 2xy = 0?
If m and n are the order and degree of the differential equation
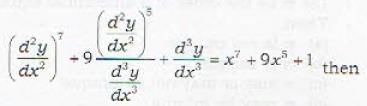
If m and n be the order and degree of the differential equation
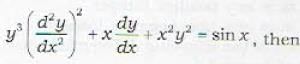
Which of the following differential equations of first order and second degree?
The solution of the differential equation 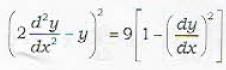 is given by
is given by
Which of the following is a solution of the differential equation 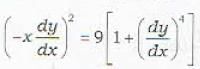
Which of the following solutions of the differential equation 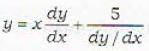 is a singular solution?
is a singular solution?
A singular solution of the given differential equation is
Which one of the following is a differential equation of the family of curves y = Ae2x + Be2x for different values of A and B?
|
27 docs|150 tests
|




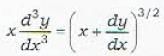
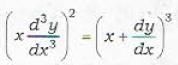

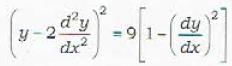

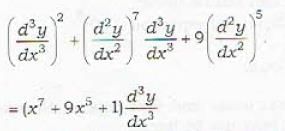
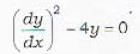 ..(i)
..(i)