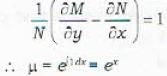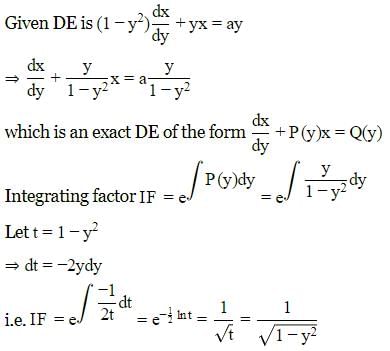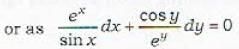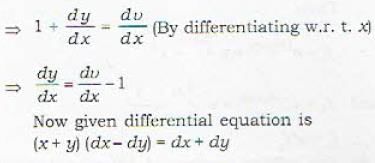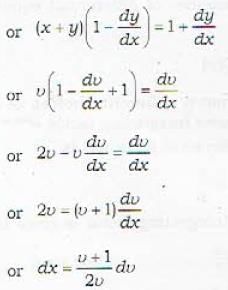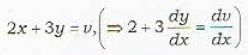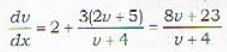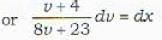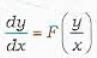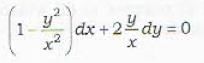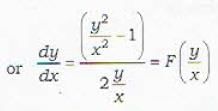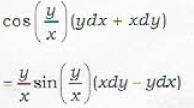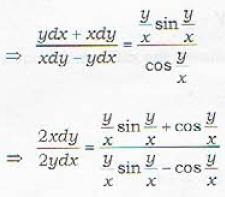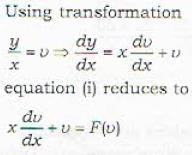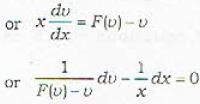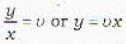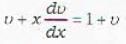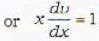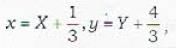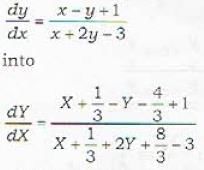Differential Equations - 17 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Differential Equations - 17
If I1 and I2 be the integrating factors of the differential equations (1 + xy)ydx + (1 - xy)xdy = 0 and (x2y - 2xy2)dx - (x3 - 3x2y)dy = 0 respectively, then
The integrating factor of differential equation (xy sin xy + cos xy)ydx + (xy sin xy - cos xy)xdy = 0 is
The integrating factor of the differential equation (x3 + y2 + 2x)dx + 2ydy = 0 is
Which of the following differential equations is with separated variables?
Which of the following differential equations is with separated variables?
The differential equation (x + y) [dx - dy] = dx + dy which is not with separated variables, can be transformed into one which is with separated variables, by the substitution
The differential equation 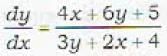 which is not with separated variables, can be transformed into one which is with separated variables, by the substitution.
which is not with separated variables, can be transformed into one which is with separated variables, by the substitution.
Which of the following differential equations is not homogeneous one?
The solution curves of the given differential equation xdx + ydy = 0 are given by a family of
The solution eurves of the given differential equation xdx - dy = 0 are given by a family of
A first order first degree homogeneous differential equation
A first order first degree homogeneous differential equation
Which of the following transformations reduces a homogeneous differential equation of first order and first degree into one with separated variables?
The transformation y = vx reduces the given homogeneous differential equation 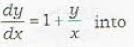
Which of the following transformations reduces the given differential equation 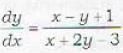 in to homogeneous one?
in to homogeneous one?
Which of the following differential equations is linear, homogeneous and of first order?
The integrating factor of the differential equation 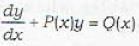 depends upon
depends upon
|
27 docs|150 tests
|