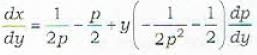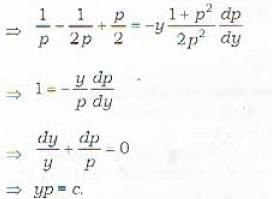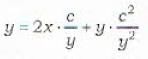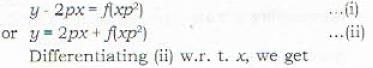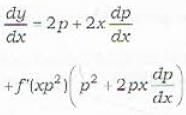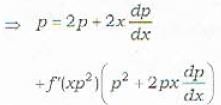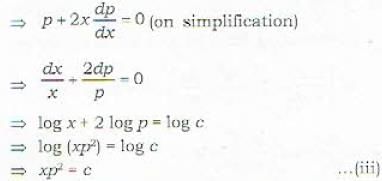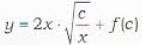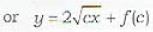Differential Equations - 18 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Differential Equations - 18
If f1 and f2 be the integrating factors of the differential equations  respectively,
respectively,
 respectively,
respectively,The integrating factor of the differential equation 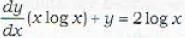 is given by
is given by
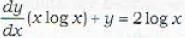 is given by
is given byThe integrating factor of the differential equation 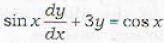 is calculated as
is calculated as
Which of the following transformations reduces the differential equation 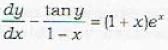 sec y into the form
sec y into the form 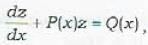 by the substitution
by the substitution
Which of the following transformations reduces the differential equation 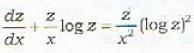 into the form
into the form 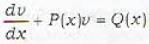 by the substitution
by the substitution
The transformation v = 1/y transforms which the following differential equations into the form

The general solution of the differential equation  where φ is a function of x alone, is given by
where φ is a function of x alone, is given by
Solution of differential equation xdy−ydx=0 represents:
The solution of the differential equation dy = (1 + y2)dx
A curve is called an isogonal trajectoiy or an x trajectory of family f(x, y, c) = 0 if
In order to find a family of orthogonal trajectories of the family of curves 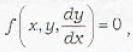 which of the following replacements is made
which of the following replacements is made
The orthogonal trajectories of the given family of curves y = cx2 are given by
Which one of the following is a general solution of the differential equation xp2 + (y - x)p - y = 0 where 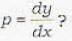
Which one of the following is a general solution of the differential equation p2 - 2p cos hx + 1 = 0?
Which one of the following is a general solution of the differential equation y = 2px + p2y ?
Which one of the following is a general solution of the differential equation y - 2px = f(xp2)?
The differential equation of the form y = x F(p) + f(p) is known as
|
27 docs|150 tests
|


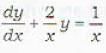 ......(i)
......(i)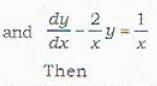
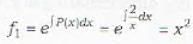
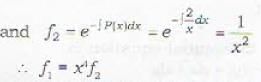
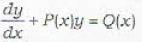
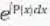

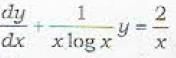
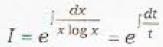 [log x = t]
[log x = t]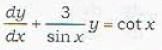

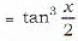
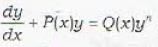 is known a
is known a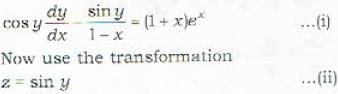
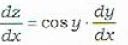
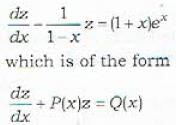
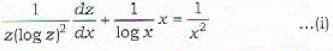
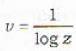
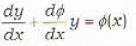 .....(i)
.....(i)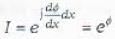
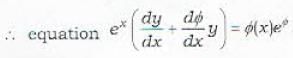
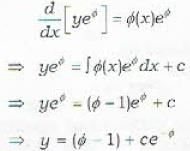
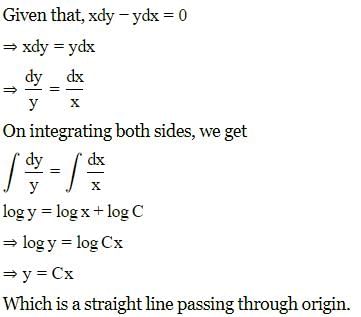
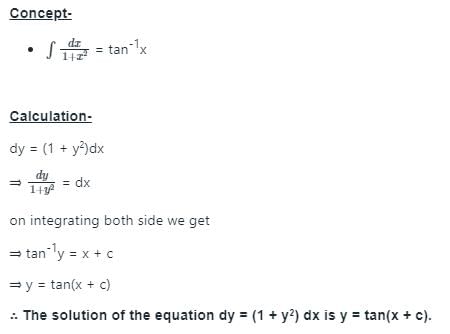
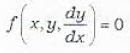 .....(i)
.....(i)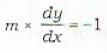
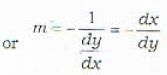

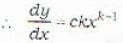
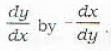
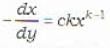
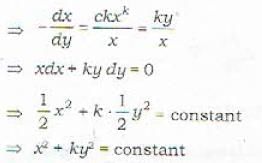

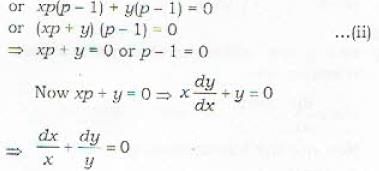
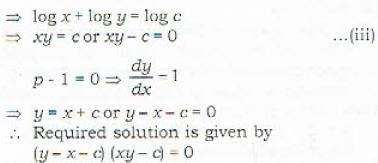
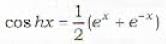
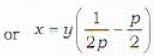 ... (iv)
... (iv)