Differential Equations - 4 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Differential Equations - 4
Let a, b ∈ R. Let y = (y1, y2)T be a solution of the system of equations

Every solution y(x) → 0 as x → ∞ if

Every solution y(x) → 0 as x → ∞ if
For  solving by variation of parameters. The value of Wronskion W is
solving by variation of parameters. The value of Wronskion W is
 solving by variation of parameters. The value of Wronskion W is
solving by variation of parameters. The value of Wronskion W is Consider the following statements
I. A singular solution of differential equation satisfies the differential equation but is not a particular solution of the equation.
II. If T(x, y) = 0 is the equation of the tac-locus, then
T(x, y ) is a factor of the P-discriminant.
III. T(x, y ) is a factor of a c-discriminant.
IV. Cusp-locus has two distinct tangent.
Choose the correct answer.
Singular solution of differential equation contains
I. arbitrary constant
II. can be obtained from general
III. do not contain arbitrary constant
IV. cannot be obtained from general solution
For non-homogeneous equation y' + p(x)y = r(x), if y1 and y2 are its solutions, then the solution of homogeneous equation y' + p(x)y = 0 is
Consider the differential equation (x + y + 1) dx + (2x + 2y + 1)dy = 0. Which of the following statement is true?
The orthogonal trajectory of the family x2 - y2 = C2 are given by
A. Singular solution contains no arbitrary constants.
B. Singular solution can be obtained from complete primitive.
Let the general solution of a differential equation be, y = aebx+c then order of the differential equation is,
If y1(x) = x and y2(x) = xex are two linearly independent solutions of 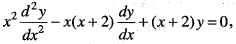 then the interval on which they form a fundam ental set of solution is
then the interval on which they form a fundam ental set of solution is
Using the method of variation of parameters for the particular solution to the differential equation
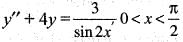
The general solution of the system of differential equation 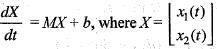 and M a 2 x 2 matrix
and M a 2 x 2 matrix  and a 2 x 1 constant vector b =
and a 2 x 1 constant vector b = 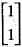 is given by
is given by
For the ordinary differential equation
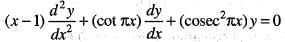
which of the following statement is true?
If 2x(1 - y ) = K and g(x, y) = L are orthogonal families of curves where K and L constants, then g(x, y) is
If y1 and y2 are linearly independent solutions of the homogeneous equation L(y) =y"+p1(x)y' + p2(x)y = 0. Then, p1(x) and p2{x) are given by
|
27 docs|150 tests
|


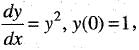 exists for all
exists for all 


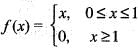 andy(0) = 0 is
andy(0) = 0 is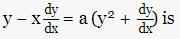
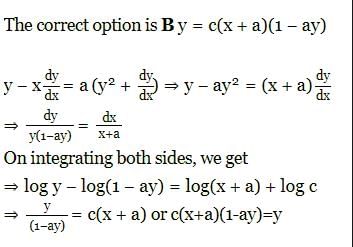
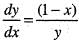 represents
represents













