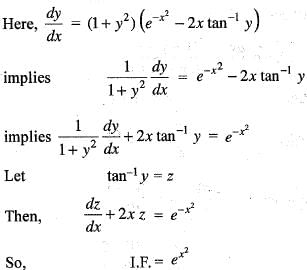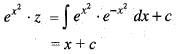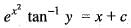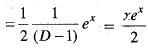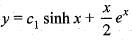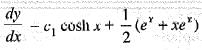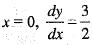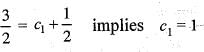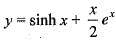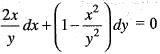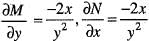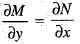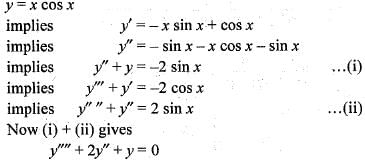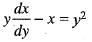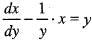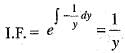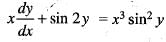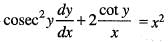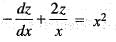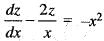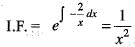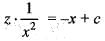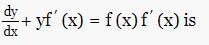Differential Equations - 6 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Differential Equations - 6
The differential equation representing the family of circles touching y - axis at the origin is
If e2x and xe2x are particular solutions of a second order homogeneous differential equation with constant coefficients, then the equation is
If ya is an integrating factor of the differential equation 2xy dx - (3x2 - y2) dy = 0, then the value of a is
If k is a constant such that 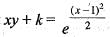 satisfies the differential equation
satisfies the differential equation 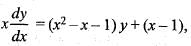 then k is equal to
then k is equal to
The solution y(x) of the differential equations 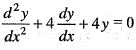 satisfying the conditions y(0) = 4,
satisfying the conditions y(0) = 4, 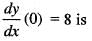
Let y1(x) and y2(x) be twice differentiable functions on a interval I satisfying the differential equations 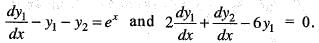 Then y1(x) is
Then y1(x) is
The solution of the differential equation 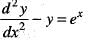 satisfying y(0) = 0 and dy/dx (0) = 3/2 is
satisfying y(0) = 0 and dy/dx (0) = 3/2 is
An integrating factor of the differential equation 2xy dx + (y2 - x2) dy = 0 is
If y = x cos x is a solution of an nth order linear differential equation 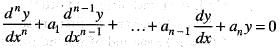 with real constant coefficients, then the least possible value of n is
with real constant coefficients, then the least possible value of n is
Let W[y1(x), y2(x)] is the Wronskian formed for the solutions y1(x) and y2(x) of the differential equation y" + a1y' + a2y = 0. If W ≠ 0 for some x = x0 in [a, b] then
Solution of the differential equation xy' + sin 2y = x3 sin2 y is
|
27 docs|150 tests
|


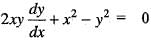
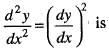
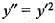

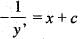

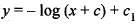
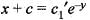
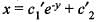


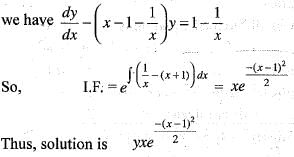
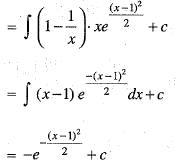
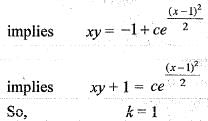
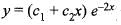
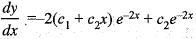
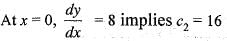
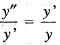
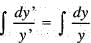
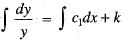
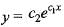
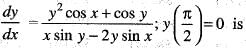
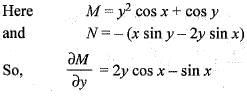
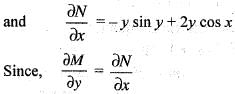
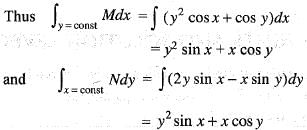
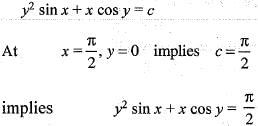
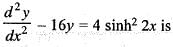
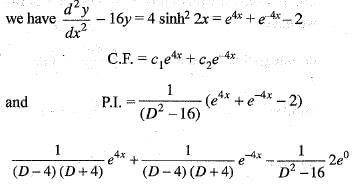
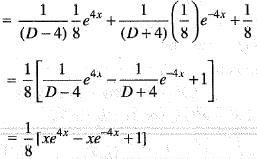
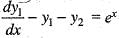
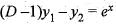 ...(i)
...(i)
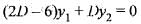 ...(ii)
...(ii)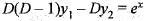 ...(iii)
...(iii)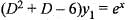
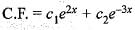
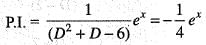
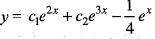
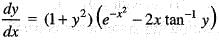 is
is