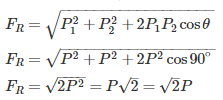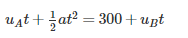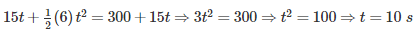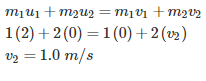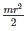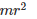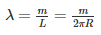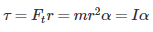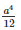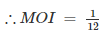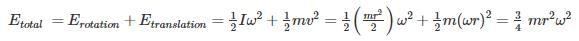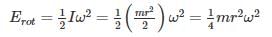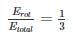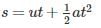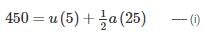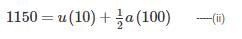Engineering Mechanics - 1
20 Questions MCQ Test Mock Test Series for SSC JE Mechanical Engineering | Engineering Mechanics - 1
| 1 Crore+ students have signed up on EduRev. Have you? |
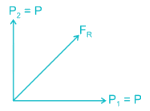
The resultant of two forces each equal to P and acting at right angles is:
Which of the following conditions do not change the effect of couple?
Two parallel forces equal in magnitude and opposite in direction and separated by a definite distance are said to form a couple.
The translatory effect of a couple on the body is zero.
The only effect of a couple is a moment and this moment is same about any point, the effect of a couple is unchanged if:
(i) The couple is rotated through any plane
(ii) The couple is shifted to any other position
(iii) The couple is replaced by another pair of forces whose rotational effect is same
Two car A and B moves at 54 Km/hr in the same direction and the car B is 300 m ahead of car A. If the car A is accelerated at 6 m/s2 while car B continue to move with the same velocity, calculate the time taken by car A to overtake car B:
uA = uB = 54 Km/hr = 15 m/s; aA = 6 m/s2, aB = 0
Car B is 300 m ahead of car A.
Let both move in time t sec.
Distance travelled by A in time t = 300 + Distance travelled by B in time t
A couple consists of two parallel forces that are equal in magnitude, opposite in sense and do not share a line of action. It does not produce any translation, only rotation. The resultant force of a couple is zero. But, the resultant of a couple is not zero; it is a pure moment.
A ball of mass 1 kg moving with the velocity of 2 m/s collide directly with another stationary ball of mass 2 kg and comes to rest after impact. The velocity of second baII after impact is:
Conservation of linear momentum: 
Collinear Forces: Line of action of all the forces act along the same line.
Coplanar parallel forces: All forces are parallel to each other and lie in a single plane
Coplanar concurrent forces: Line of action of all forces pass through a single point and forces lie in the same plane
Coplanar non-concurrent forces: All forces do not meet at a point, but lie in a single plane
Non-coplanar parallel forces: All the forces are parallel to each other, but not in same plane
Non-coplanar concurrent forces: All forces do not lie in the same plane, but their lines of action pass through a single point
Non-coplanar non-concurrent forces: All forces do not lie in the same plane and their lines of action do not pass through a single point
Two rings of radius R and nR, made up of same material (linear mass density) have the ratio of moment of inertia about an axis passing through centre as 1 : 8. The value of n is
For ring:
MOI about diametric axis: 
MOI about polar axis: 
Linear mass density:
m=λ×2πR
n = 2
A 13 m ladder is placed against a smooth vertical wall with its lower end 5 m from the wall. What should be the coefficient of friction between the ladder and floor so that it remains in equilibrium?
Without knowing the weight of the ladder, coefficient of friction between the ladder and floor cannot be found.
The torque acting on a body, rotating with angular acceleration of ‘α’ is given by which of the following relation?
Ft=mat=mrα
A 1.0 kg ball drops vertically onto the floor with a speed of 25 m/s. It rebounds with an initial speed of 10 m/s. The impulse action on the ball during contact will be
Impulse = change in momentum
= mv2 - mv1
= 1 (10) - 1 (-25) = 35 N - s
The area moment of inertia of a square of size 1 unit about is diagonal is
For a square of side a, the area moment of inertia of square with respect to one diagonal is 
Here a = 1
If tension in the cable supporting a lift moving downwards is half the tension when it is moving upwards, the acceleration of the lift is
When lift is at rest: T = mg
When lift is accelerating upward: TU = mg + ma
When lift is accelerating downward: TD = mg - ma
TU = 2TD
mg + ma = 2mg - 2ma
a = g/3
The moment of inertia of a square of side (a) about an axis though its center of gravity is
Moment of inertia of a rectangle about an axis though its center of gravity is bd3/12 and of a square is a4/12.
Moment of inertia of an area always least with respect to
Mass distribution is minimum about centroidal axis, so moment of inertia of an area always least with respect to centroidal axis
Which of the following is an example of a body undergoing translational equilibrium?
An object is said to be in equilibrium when there is no external net force acting on it. When an object is in equilibrium, it does not accelerate. If it had a velocity, the velocity remains constant; if it was at rest, it remains at rest.
If all the forces acting on a particular object add up to zero and have no resultant force, then it’s in translational equilibrium. Examples would be a book resting on a bookshelf, or someone walking at a steady, constant speed.
An object that’s not rotating or doing so at a steady speed, the sum of the torques acting on it equaling zero, is at rotational equilibrium. Some examples of this are a Ferris wheel turning at a constant velocity, two children of equal weight balanced on either side of a seesaw, or the Earth rotating on its axis at a steady speed.
A circular disc rolls down an inclined plane, the fraction of its total energy associated with its rotation is _____
Total energy of the disc rolling down on an inclined plane is
Total rotational energy is
A body of mass 10 kg moving with a velocity of 1 m/s is acted upon by a force of 50 N for two seconds. The final velocity will be:
Velocity = mass × acceleration
∴ 50 = 10 × a
⇒ a = 5 m/sec2
Velocity after 2 seconds,
v = u + at
= 1 + 5 × 2
= 11 m/sec
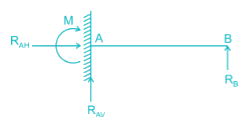
A beam is fixed at one end and is vertically supported at the other end. What is the degree of statical indeterminacy?
If the number of independent static equilibrium equations is not sufficient for solving all the external and internal forces in a system, then the system is said to be statically indeterminate.
Degree of static indeterminacy = Total no. of unknowns (External and internal) – Number of independent equations of equilibrium.
Now in this problem,
No. of unknowns = 4 (RAH, RAV, M and RB)
No. of independent equations of equilibrium = 3 (∑H = 0, ∑V = 0, ∑M = 0)
∴ Degree of static indeterminacy - 4 - 3 = 1
The angular motion of a disc is defined by the relation (θ = 3t + t3), where θ is in radians and t is in seconds. What will be the angular position after 2 seconds?
Angular motion θ = 3t + t3
Motion covered in 2 seconds = 3 * 2 + 23 = 14 rad. So the angular position after 2 seconds will be 14 rad.
A car moving with uniform acceleration cover 450 m in a 5 second interval, and covers 700 m in the next 5 second interval. The acceleration of the car is
at t = 5 sec, s = 450 m
at t = 10 sec
s = 450 + 700 = 1150
Equation (ii) – Equation (i), we get
a = 10 m/s2
|
3 videos|1 docs|55 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
3 videos|1 docs|55 tests
|
Download free EduRev App
Related content with Engineering Mechanics - 1
|
|
|
|
Related tests with Engineering Mechanics - 1
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
