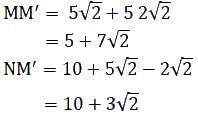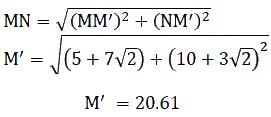GATE Numerical Reasoning Aptitude (Analytical) Questions - 2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - GATE Numerical Reasoning Aptitude (Analytical) Questions - 2
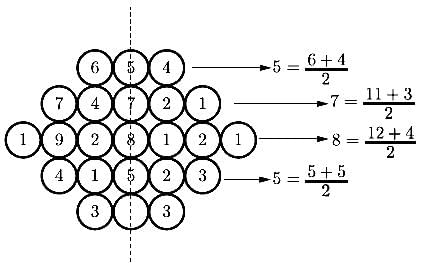
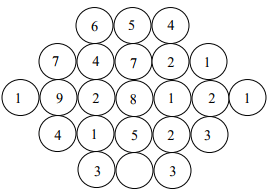
Fill in the missing value

Given (9 inches)1/2 = (0.25 yards) 1/2, which one of the following statements is TRUE?
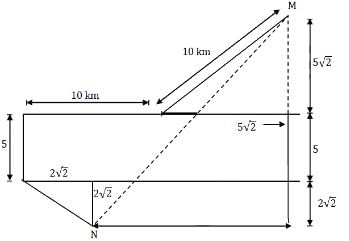
M and N start from the same location. M travels 10 km East and then 10 km North-East. N travels 5 km South and then 4 km South-East. What is the shortest distance (in km) between M and N at the end of their travel?
The number that least fits this set: (324, 441, 97 and 64) is _____.
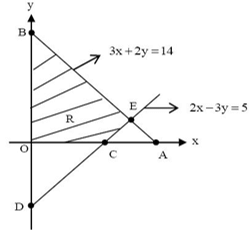
Find the area bounded by the lines 3x + 2y = 14, 2x - 3y = 5 in the first quadrant.
A straight line is fit to a data set (ln x, y). This line intercepts the abscissa at ln x = 0.1 and has a slope of −0.02. What is the value of y at x = 5 from the fit?
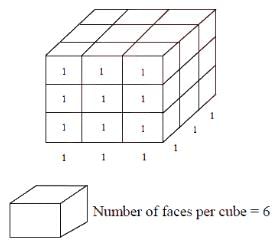
A cube of side 3 units is formed using a set of smaller cubes of side 1 unit. Find the proportion of the number of faces of the smaller cubes visible to those which are NOT visible.
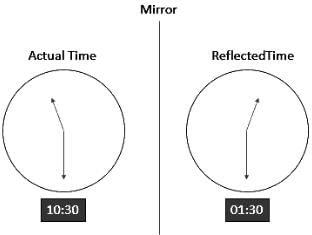
Two and a quarter hours back, when seen in a mirror, the reflection of a wall clock without number markings seemed to show 1:30. What is the actual current time shown by the clock?
A wire of length 340 mm is to be cut into two parts. One of the parts is to be made into a square and the other into a rectangle where sides are in the ratio of 1:2. What is the length of the side of the square (in mm) such that the combined area of the square and the rectangle is a MINIMUM?
It takes 10s and 15s, respectively, for two trains travelling at different constant speeds to completely pass a telegraph post. The length of the first train is 120 m and that of the second train is 150 m. The magnitude of the difference in the speeds of the two trains (in m/s) is _____.