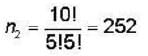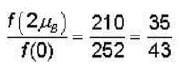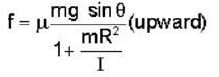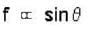GATE Physics Mock Test Series - 2 - Physics MCQ
30 Questions MCQ Test - GATE Physics Mock Test Series - 2
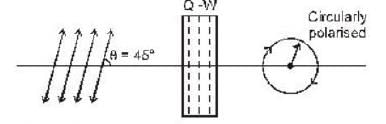
Consider a beam of plane polarised light of wavelength λ is incident on a optical component making angle 45° to the optical axis and output light is circularly polarised then the optical component is
A body of mass 2kg is moving under the influence of a central force whose potential energy is given by U=2r3J If the body is moving in a circular orbit of 5m its energy will be
A particle of mass m moves in a central force field defined by 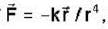 if E is the total energy supplied to the particle, then its speed is given by .
if E is the total energy supplied to the particle, then its speed is given by .
The space - time coordinates of two events as measured by O are x1= 6 * 104 m ,y1 = z1= Om, t1’ = 2 * 10-4sec and X2,= 12 x 104m, t2 = 1 x 10-4sec. What must be the velocity of O’ with respect to O if O’ measures the two events to occur simultaneously ?
The surface integral ∬ₛ F . n dS over the surface S of the sphere x² + y² + z² = 9, where F = (x + y)î + (x + z)ĵ + (y + z)k̂ and n is the unit outward surface normal, yields ________.
Fourier series which will represents f(x) = x sinx in the interval -π< x< π, then
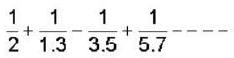
will have value
A particle moving in a central force located at r = 0 describes the spiral r = e-θ, the magnitude of force is inversely proportional to
Rest mass energy of an electron is 0.51 MeV. A moving electron has a kinetic energy of 9.69 MeV. The ratio of the mass of the moving electron to its rest mass is
A system of four particles is x - y plane. Of these, two particles each of mass m are located at (-1, 1) and (1, -1). The remaining two particles each of mass 2m are located at (1, 1) and (-1, 1). The xy component of the moment of inertia tensor of this system of particles is -
What is the energy of a uniformly charged spherical shell of total charge q and radius R.
A current I is uniformly distributed over a wire of circular cross section, with radius a, suppose the current density in the wire is proportional to the distance from the axis J = Kx (K is constant)
Find the total current in the wire
For a Gaussian wave packet described by 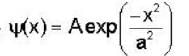 The expectations value of the momentum operator is
The expectations value of the momentum operator is
The wave function of a particle is given by ψ= c exp (-x2α2 ) , 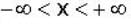 co where c and a are constants. The probability of finding the particle in the region
co where c and a are constants. The probability of finding the particle in the region 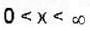
A particle is moving with one component of constant velocity parallel to the axis of y and another component of velocity parallel to the axis of x proportional to y. It will describe a
The solution of the differential equation for 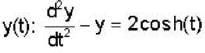 subject to the initial condition y(O) = 0 and
subject to the initial condition y(O) = 0 and 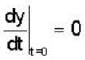 ,is
,is
What is the magnitude of the linear momentum of a photon of radiation having electric field described by e =
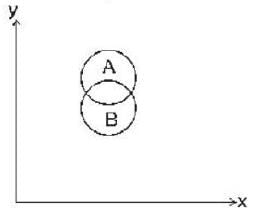
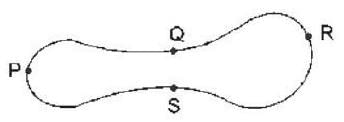
Given that the magnetic flux through the closed loop PQRSP is 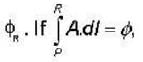 along PQR, the value of
along PQR, the value of 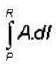 along PSR is
along PSR is
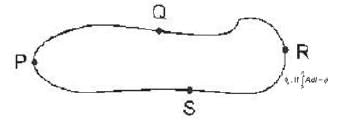
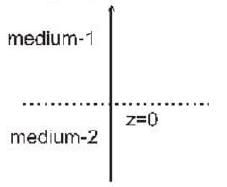
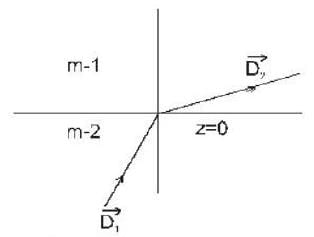
Two infinitely extended homogeneous isotropic dielectric media (medium - 1 and medium - 2 with dielectric constant 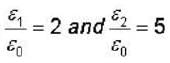 respectively) meet at the z = 0 plane as shown in the figure. A uniform electric field is given by
respectively) meet at the z = 0 plane as shown in the figure. A uniform electric field is given by 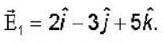 The interface separating the two media is charge free. The electric displacement vector in the medium 2 is given by
The interface separating the two media is charge free. The electric displacement vector in the medium 2 is given by
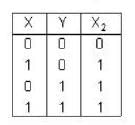
Which of the following truth table for the given logic is true?
Magnetic flux linked with a stationary loop of resistance R varies with respect to time during the time period T as follows:
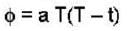
Find the amount of heat generated in the loop during that time. Inductance of the coil is negligible
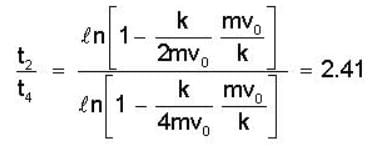
At t = 0, a particle of mass m having v0 starts moving through a liquid kept in a horizontal tube and experiences a drag force 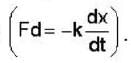 It covers a distance L before coming to rest. If the times taken to cover the distances
It covers a distance L before coming to rest. If the times taken to cover the distances 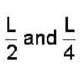 are t2 and t4, respectively, then
are t2 and t4, respectively, then
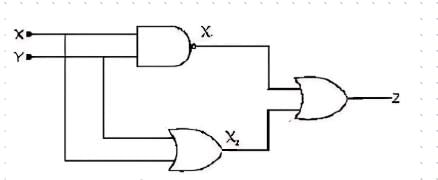
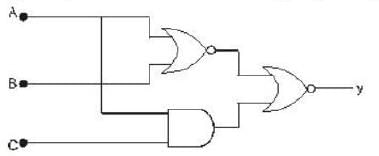
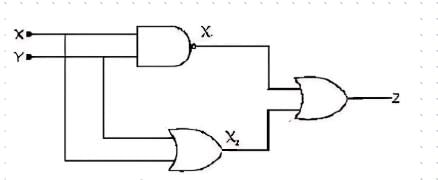
The simplified logic expression for the following logic diagram is
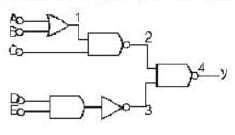
For the logic circuit shown in the figure, the output y is given by
An open pipe is suddenly closed at one end with the result that the frequency of third harmonic of the closed pipe is found to be higher by 200 H2 then the fundamental frequency of the open pipe - The fundamental frequency of the open pipe is
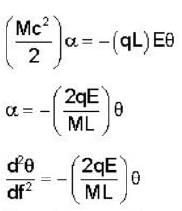
A paint particle of mass M attached to one end of a massless rigid non - conducting rod of length L. Another paint particle of the same mass is attached to the other end of the rod. The two particles carry changes + q and -q respectively. This arrangement is held in a region of a uniform electric field E such that the rod makes a small angle 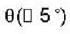 with the field direction. Find the minimum time needed for the rod to become parallel to the field after it is set free
with the field direction. Find the minimum time needed for the rod to become parallel to the field after it is set free

Which of the following statement regarding the electric fields  is correct
is correct
A system of four identical distinguishable particles has energy 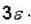 The single particle states are available at energies
The single particle states are available at energies  Find the average number n(E) of particles in energy e =
Find the average number n(E) of particles in energy e = 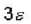
Consider 10 atoms fixed at lattices sites. Each atom can have magnetic moment 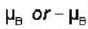 in the z - direction. Let f (μ) denote the probability that the magnetic moment of the system is μ. Assuming statistical mechanics to hold. Find the value of
in the z - direction. Let f (μ) denote the probability that the magnetic moment of the system is μ. Assuming statistical mechanics to hold. Find the value of 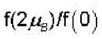
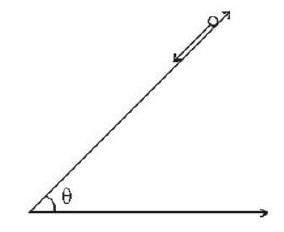
A solid sphere is in pure rolling motion on an inclined surface having inclination θ :


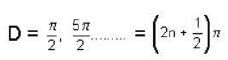
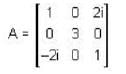
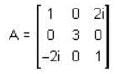
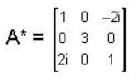
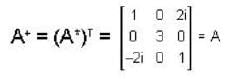

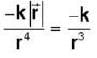
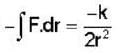
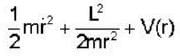
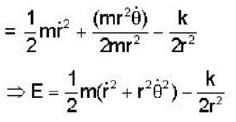
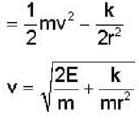
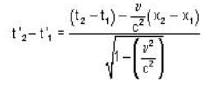
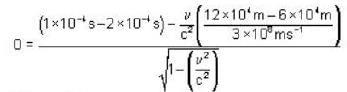
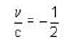



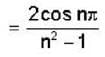
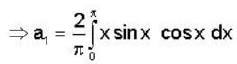
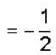
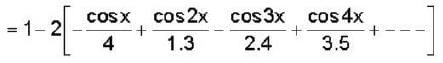
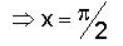
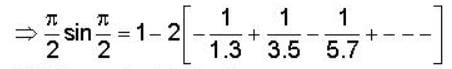
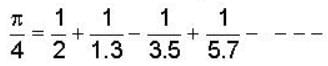
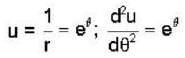
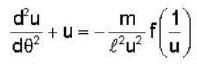

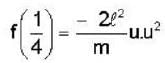
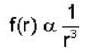
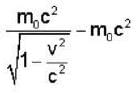
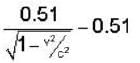
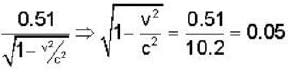
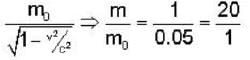
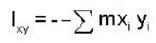

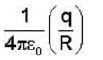
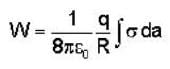
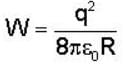
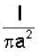
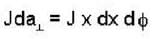
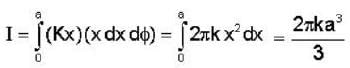
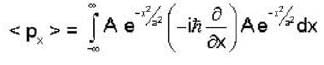
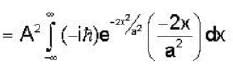
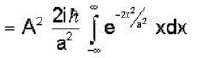
 is
is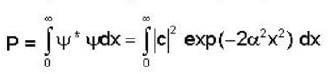

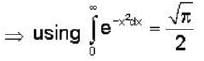
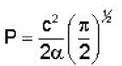
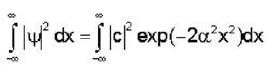
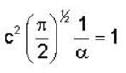

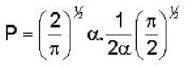
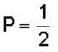
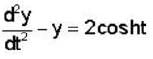
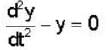
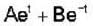
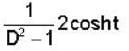
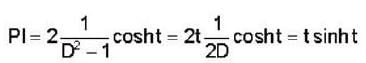
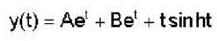
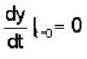
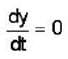
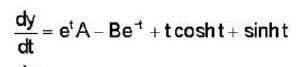
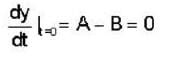
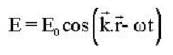
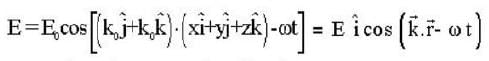
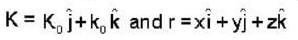
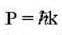
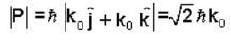
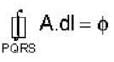
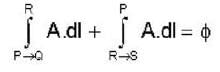
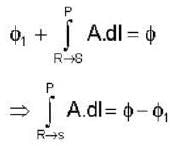
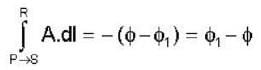
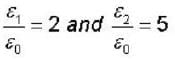

 is continuous at the boundary
is continuous at the boundary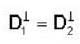
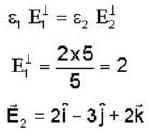
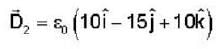
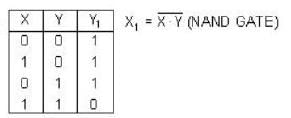

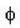 = at(T - 1)
= at(T - 1)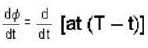
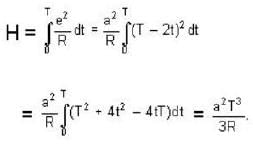
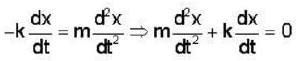
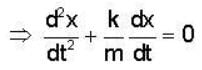
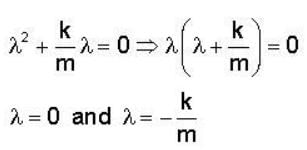
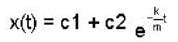
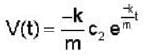
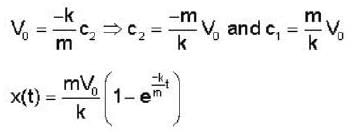
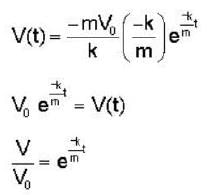
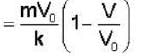
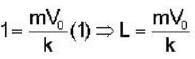


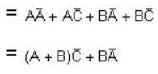
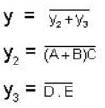
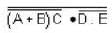
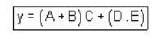
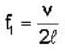 and frequency of third harmonic of closed pipe will be
and frequency of third harmonic of closed pipe will be 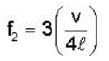
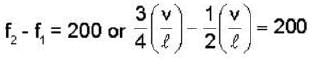
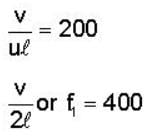

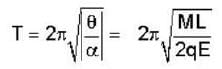
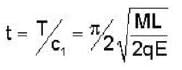
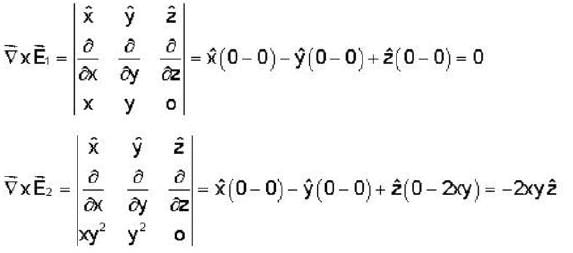
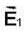 field can represent electrostatic field..
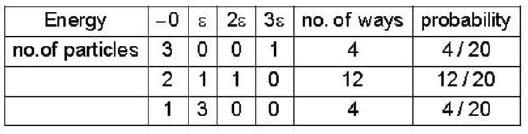
field can represent electrostatic field..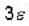 are shown in table
are shown in table 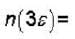
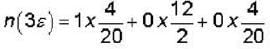
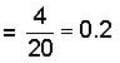
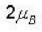 if 6 atoms in
if 6 atoms in 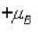 state and 4 in
state and 4 in 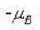 state. This can happen in n
state. This can happen in n 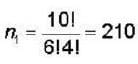
 state and five in
state and five in  state. This can happen in n2 ways where
state. This can happen in n2 ways where