Important Questions: Lines and Angles - Class 7 MCQ
15 Questions MCQ Test Mathematics (Maths) Class 7 (Old NCERT) - Important Questions: Lines and Angles
The sum of the measures of the angles in a linear pair is
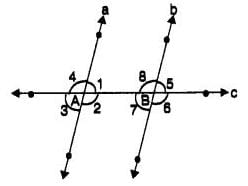
In the following figure, a transversal c intersects two parallel lines a and b at A and B respectively and the angles formed at A and B are marked. Tell which of the following pairs of angles need not be equal?

Which of the following pairs of angles form a linear pair?
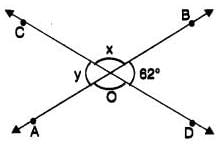
In the following figure, two straight lines AB and CD are intersecting each other at the point 0 and the angles thus formed at 0 are marked, then the value of ∠x – ∠y is
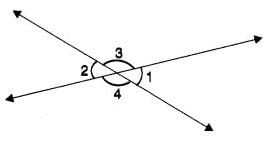
In the following figure, if ∠1 + ∠2 = 100°, then the measure of ∠4 is equal to
The measure of the supplement of the angle 120° is
Find the measure of the angle which is double of its complementary angle?
When the sum of the measures of two angles is 90°, the angles are called
The measure of the complement of the angle 30° is
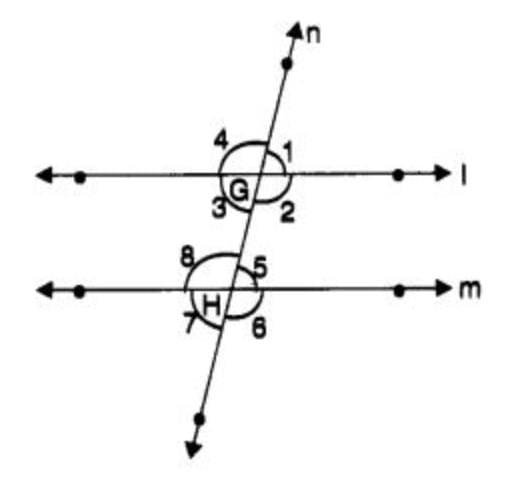
In the following figure, a transversal cuts two parallel lines l and m at points G and H respectively and the angles thus formed are marked. If ∠1 is an acute angle, then, which of the following statements is false?
Which pair of the following angles are complementary?
What will be the sum of the two angles to make it complementary?
Which pair of the following angles are not supplementary?
|
76 videos|452 docs|39 tests
|














